常見(jiàn)的, 物體/圖片做拋物線或者更準(zhǔn)確的說(shuō)是沿貝塞爾曲線運(yùn)動(dòng)是H5開(kāi)發(fā)中常見(jiàn)的需求, 那么如何快速的根據(jù)設(shè)計(jì)稿計(jì)算出運(yùn)動(dòng)路徑是開(kāi)發(fā)者首要解決的問(wèn)題.

我這邊H5開(kāi)發(fā)常用的設(shè)計(jì)稿尺寸是640 * 1008, 那么根據(jù)這個(gè)尺寸解決方案思路如下:

1, 首先將PS中要位移的元素單獨(dú)導(dǎo)出一張png, 如果設(shè)計(jì)稿中已經(jīng)規(guī)劃好了運(yùn)動(dòng)路線的話也需要將該路線導(dǎo)出為png;

2, 在AI中新建一個(gè)和設(shè)計(jì)稿尺寸一樣的文件,再將位移元素分兩次拖入該文件中, 如果有運(yùn)動(dòng)路線的話也拖入進(jìn)去,如下所示:

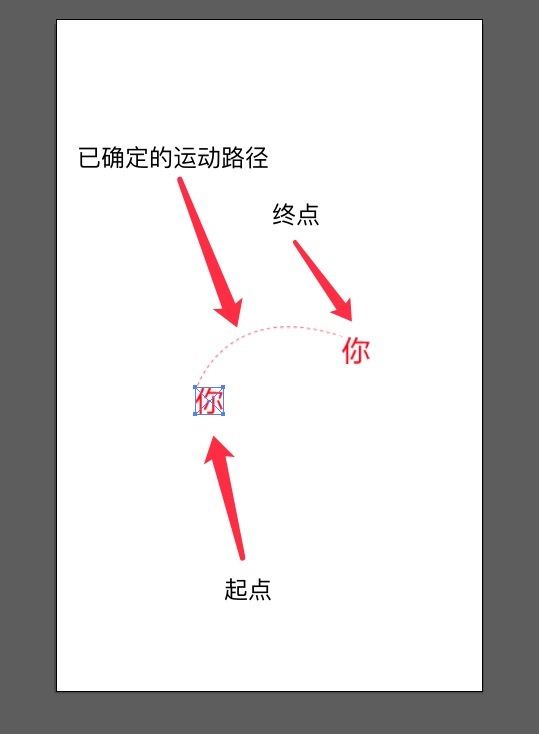
這里需要注意的是位移圖片的擺放位置, 路徑的起點(diǎn)和終點(diǎn)應(yīng)該對(duì)應(yīng)著圖片的移動(dòng)點(diǎn).對(duì)應(yīng)的情況有如下幾種:

1. canvas中不做變形處理, 那么移動(dòng)點(diǎn)就是圖片的左上角
2. canvas中, 圖片做了translate移動(dòng), 因根據(jù)translate(x1, y1)中的x1, y1去加上drawImage(image, sx, sy, sWidth, sHeight, dx, dy, dWidth, dHeight)中dx和dy的最終偏移.
3. 如果元素通過(guò)position:absolute定位, 并通過(guò)transform中translate3d(x, y, z)來(lái)控制位置的話,偏移量應(yīng)該是x, y. 通常的, transform中我們有可能模仿 left, top和額外的margin來(lái)控制元素的位置, 在transform中額外的添加一個(gè)translate3D(marginLeftX, marginLeftY, 0). 也需要把這個(gè)margin的值考慮進(jìn)去.

3, 在AI中通過(guò)ctrl + r鍵拉出參考線, 在元素圖片的移動(dòng)拉出其x, y的位置, 如下圖所示:

然后選擇鋼筆工具, 先后在起點(diǎn)和終點(diǎn)處點(diǎn)擊, 在點(diǎn)擊終點(diǎn)后鼠標(biāo)不要松開(kāi), 直接拖動(dòng)AI會(huì)自動(dòng)添加2個(gè)控制點(diǎn). 通過(guò)移動(dòng)鼠標(biāo)可以調(diào)整兩個(gè)控制點(diǎn)的位置, 從而達(dá)到調(diào)整鋼筆工具所生成的路徑的目的, 直到和設(shè)計(jì)稿上的參考線路徑一致.如下所示:

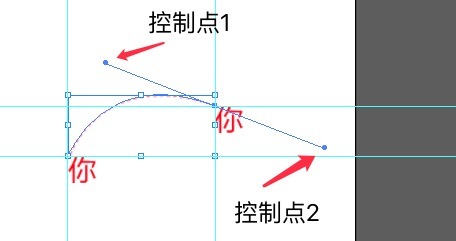
拖到想要的位置后, 松開(kāi)鼠標(biāo), 鍵盤回車確定路徑, 如果所勾勒的路徑不合心意還可以繼續(xù)拖動(dòng)控制點(diǎn)以作調(diào)整.

4, 在調(diào)整完畢后, 額外的拖動(dòng)兩條參考線到控制點(diǎn)1的位置, 然后通過(guò) 菜單欄 -- 窗口 -- 信息, 打開(kāi)信息面板, 分別將起點(diǎn), 控制點(diǎn), 終點(diǎn), 3個(gè)點(diǎn)的坐標(biāo)取出來(lái).

5, 分別計(jì)算控制點(diǎn), 終點(diǎn)和起點(diǎn)的像素差, 根據(jù)H5中要位移的圖片的真實(shí)x, y的坐標(biāo)值和像素差做計(jì)算得出真實(shí)的控制點(diǎn), 終點(diǎn)坐標(biāo). 再將這三個(gè)坐標(biāo)點(diǎn)應(yīng)用于公式中即可.

其中, 參數(shù)分別是getBezierPath(終點(diǎn), 控制點(diǎn)1, 控制點(diǎn)2, 起點(diǎn), 運(yùn)動(dòng)次數(shù)), 如果沒(méi)有控制點(diǎn)2, 直接講終點(diǎn)的坐標(biāo)填進(jìn)去即可._getBezierPath最終公式如下:

function getBezierPath(p1, p2, p3, p4, times) {
    function Point2D(x,y){  
        this.x = x || 0.0;  
        this.y = y ||0.0;  
    }  
    
    function PointOnCubicBezier( cp, t ) {  
        var   ax, bx, cx;  
        var   ay, by, cy;  
        var   tSquared, tCubed;  
        var   result = new Point2D ;  
        cx = 3.0 * (cp[1].x - cp[0].x);  
        bx = 3.0 * (cp[2].x - cp[1].x) - cx;  
        ax = cp[3].x - cp[0].x - cx - bx;        
        cy = 3.0 * (cp[1].y - cp[0].y);  
        by = 3.0 * (cp[2].y - cp[1].y) - cy;  
        ay = cp[3].y - cp[0].y - cy - by;        
        tSquared = t * t;  
        tCubed = tSquared * t;        
        result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;  
        result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;        
        return result;  
    }  
    function ComputeBezier( cp, numberOfPoints, curve ){  
        var   dt;  
        var   i;        
        dt = 1.0 / ( numberOfPoints - 1 );  
         for( i = 0; i < numberOfPoints; i++)  
            curve[i] = PointOnCubicBezier( cp, i*dt );  
    }  
      
    var cp=[  
        new Point2D(parseInt(p4[0]), parseInt(p4[1])), new Point2D(p2[0], p2[1]), new Point2D(p3[0], p3[1]), new Point2D(p1[0], p1[1])  
    ];  
    var numberOfPoints = times;  
    var curve=[];  
    ComputeBezier( cp, numberOfPoints, curve );  
    return curve;
}

以上就是本文的全部?jī)?nèi)容，希望對(duì)大家的學(xué)習(xí)有所幫助，也希望大家多多支持腳本之家。