二叉樹簡介
關于樹的介紹,請參考:https://www.jb51.net/article/222488.htm
一、二叉樹簡介
二叉樹是每個節點最多有兩個子樹的樹結構,是一種特殊的樹,如下圖,就是一棵二叉樹。
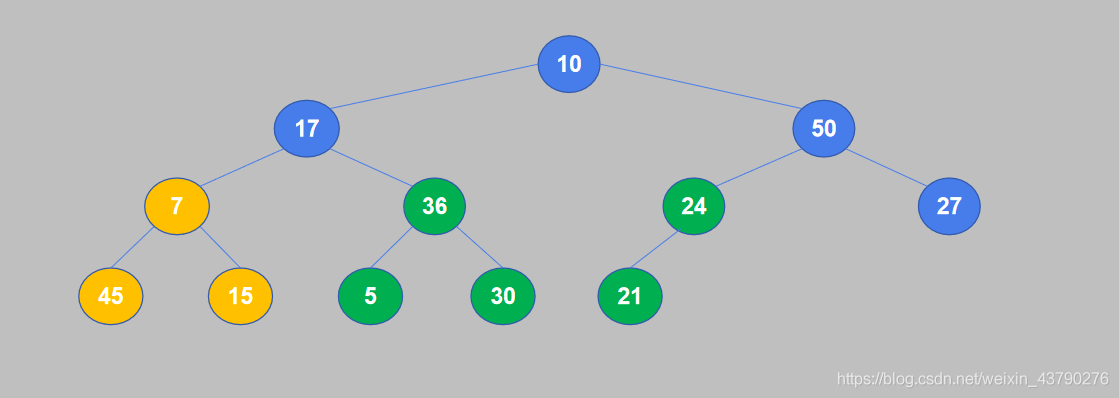
二叉樹是由n(n>=0)個節點組成的數據集合。當 n=0 時,二叉樹中沒有節點,稱為空二叉樹。當 n=1 時,二叉樹只有根節點一個節點。當 n>1 時,二叉樹的每個節點都最多只能有兩個子樹,遞歸地構建成一棵完整的二叉樹。
二叉樹的兩個子樹被稱為左子樹(left subtree)和右子樹(right subtree)。在二叉樹中,如果節點沒有子樹,則左子樹和右子樹都為空,如果節點只有一個子樹,要根據子樹的左右來區分子樹是左子樹還是右子樹,如果節點有兩個子樹,則左子樹和右子樹都有。
如果,樹中存在一個節點,該節點的子樹超過兩個,則該樹不是二叉樹,如下圖中,節點C有三個子樹,所以這不是一棵二叉樹。
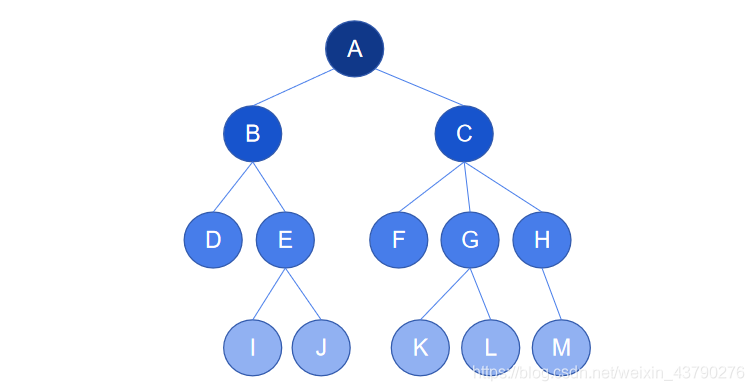
二、幾種特殊的二叉樹
只要樹中所有節點的子樹都不超過兩個(0個,1個,2個),這就是一棵普通的二叉樹。在二叉樹中,有一些比較特殊,除了滿足二叉樹的結構外,還滿足一些特殊的規則,主要有如下幾種。
1. 完全二叉樹:假設一棵二叉樹的深度為d(d>1),除了第d層外,其它各層的節點數目均已達最大值,且第d層所有節點從左向右連續地緊密排列,這樣的二叉樹被稱為完全二叉樹。
完全二叉樹的葉節點只能出現在最下層和次下層,最下層的葉節點靠左緊密地排列,次下層如果存在葉節點,葉節點緊密地靠右排列。
如下圖,樹的深度為4,除了第4層,節點數達到了最大(“掛滿了”),第4層的節點都是緊密地靠左排列(中間沒有空位),所以這是一棵完全二叉樹。
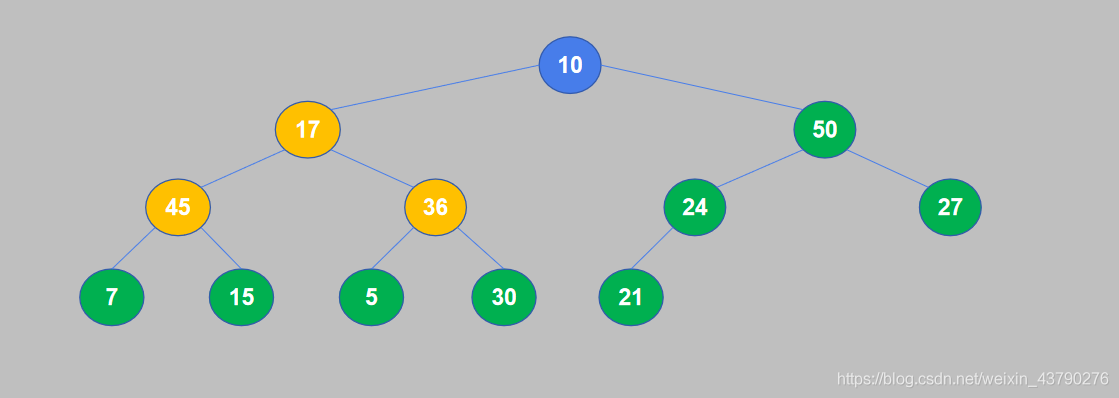
如下圖,樹的深度也為4,除了第4層,節點數也達到了最大,但是第4層的節點不是緊靠左側排列的(節點E沒有子節點,空了兩個位置),所以這不是一棵完全二叉樹,只是一棵普通的二叉樹。
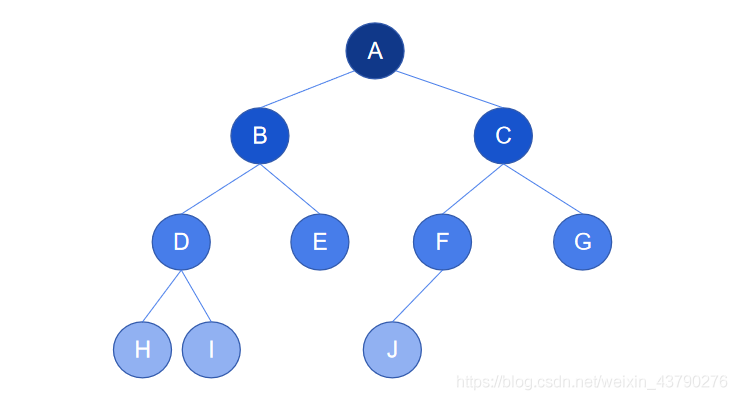
2. 滿二叉樹:所有葉節點都在最底層的完全二叉樹稱為滿二叉樹。滿二叉樹是完全二叉樹中的特殊情況,除了滿足完全二叉樹的特征,還滿足所有葉節點都在最底層。滿二叉樹是相同深度的二叉樹中葉節點最多的樹。
如下圖,這首先是一棵完全二叉樹,其次,所有的葉節點都在最底層,所以這是一棵滿二叉樹。其實,滿二叉樹也可以這么定義,二叉樹有節點的所有層,節點數目均已達最大值,則這是一棵滿二叉樹。
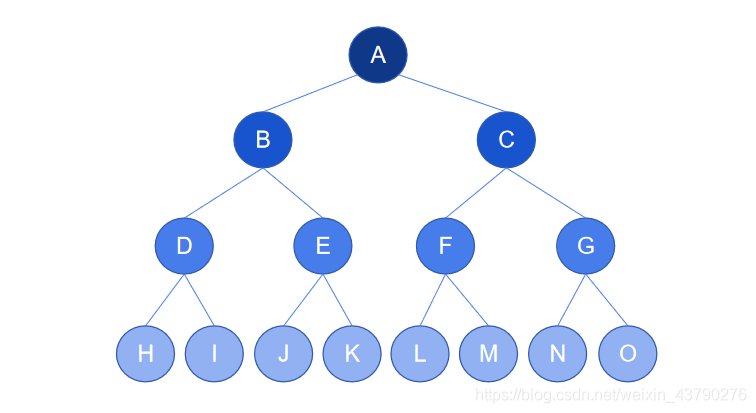
3. 平衡二叉樹(AVL樹):如果二叉樹的所有節點的兩棵子樹的高度差不大于1,則二叉樹被稱為平衡二叉樹。
如上圖中的滿二叉樹,任何節點的兩棵子樹高度差都是0(高度都相等,高度差不大于1),所以這是一棵平衡二叉樹。
如下圖中的二叉樹,對于根節點A,左子樹是以節點B為根的子樹,高度為4,右子樹是以節點C為根的子樹,高為2,A的左子樹與右子樹的高度差為2(高度差大于1),所以這不是一棵平衡二叉樹。
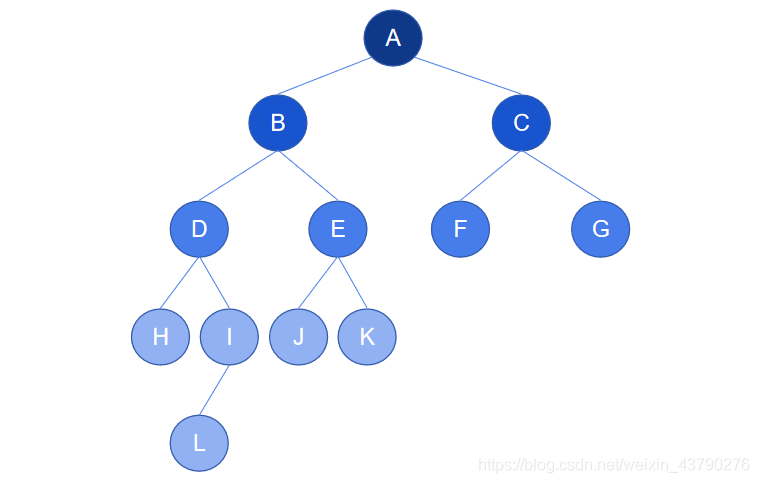
AVL樹得名于它的發明者G. M. Adelson-Velsky和E. M. Landis,是兩人姓的縮寫。AVL樹中任何節點的兩個子樹的高度差不大于1,通過高度來判斷是否平衡,所以也被稱為高度平衡樹。
4. 排序二叉樹(二叉查找樹,Binary Search Tree):又稱為二叉搜索樹、有序二叉樹。
排序二叉樹需要具有如下的性質:
4.1 如果二叉樹的左子樹不為空,則左子樹上所有節點的值均小于它的根節點的值。
4.2 如果二叉樹的右子樹不為空,則右子樹上所有節點的值均大于它的根節點的值。
4.3 如果獨立地看,左子樹、右子樹也分別為排序二叉樹,用遞歸的思想,直到樹的葉節點。
如下圖,根節點8的左子樹中,所有節點的值都小于根節點,右子樹中,所有節點的值都大于根節點,并且左子樹和右子樹都是排序二叉樹,所以這是一棵排序二叉樹。

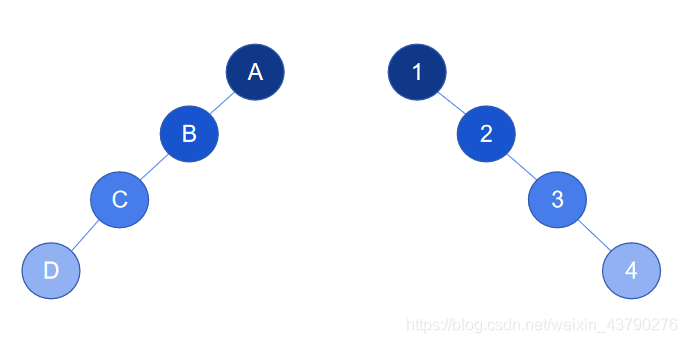
5. 斜樹:除了葉節點,所有節點都只有左子樹的二叉樹稱為左斜樹。除了葉節點,所有節點都只有右子樹的二叉樹稱為右斜樹。他們統稱為斜樹,判斷二叉樹是否為斜樹,主要是看樹的結構,對節點的值沒有要求。
如下圖,左邊的樹中,除了葉節點D,所有節點都只有左子樹,這是一棵左斜樹,同理,右邊的樹是一棵右斜樹。
三、二叉樹的特點和性質
通過對二叉樹的介紹和對幾種特殊二叉樹的了解,可知二叉樹有以下特點:
1. 每個節點最多有兩顆子樹,所以二叉樹中節點的度不大于2,二叉樹的度也不會大于2。
2. 左子樹和右子樹的次序不能顛倒。
3. 即使某節點只有一棵子樹,也要根據左右來區分它是左子樹還是右子樹。
此外,二叉樹還具有如下性質:
1. 在二叉樹的第i層,至多有 2^(i-1) 個節點(i>0) 。
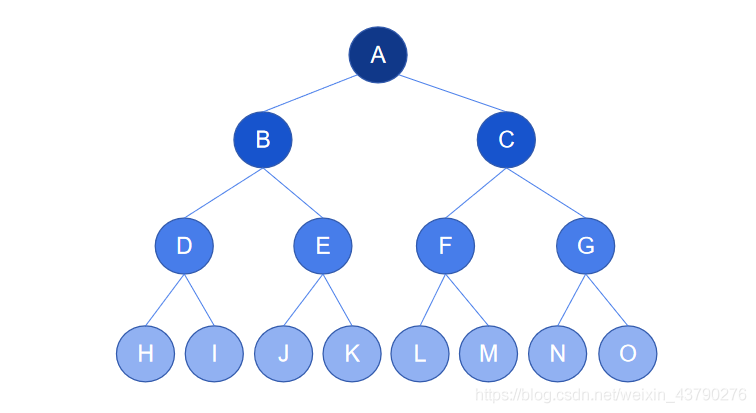
這里說的是至多的情況,滿二叉樹的每一層節點都“掛滿”了,所以可以用下圖中的滿二叉樹來驗證,第1層的節點數為2^(1-1)=1個,... 第4層的節點個數最多為 2^(4-1)=8個。
2. 深度為i的二叉樹至多有 2^i - 1 個節點(k>0) 。
這里也是說至多的情況,所以也用滿二叉樹來驗證,深度為4時,二叉樹的節點數最多為 2^4 - 1=16-1=15個。
3. 對于任意一棵二叉樹,如果其葉節點數為M,度為2的節點總數為N,則 M=N+1 。
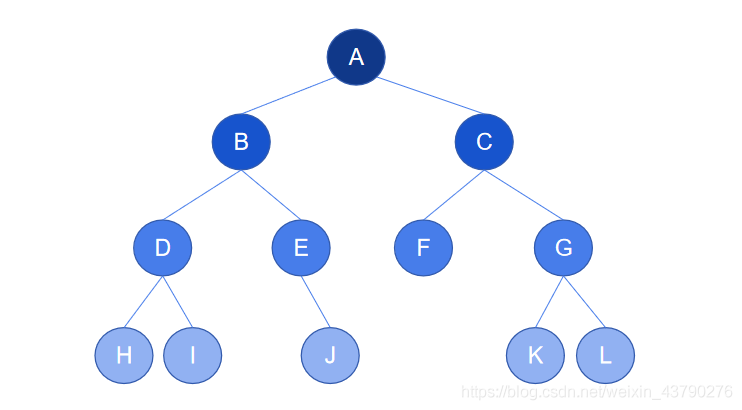
為了不失一般性,下圖中的樹是一棵普通的二叉樹,葉節點為 F,H,I,J,K,L ,共6個,度為2的節點為 A,B,C,D,G ,共5個。
4. 具有n個節點的滿二叉樹的深度必為 log2(n+1) 。這個性質是上面第2點的逆運算。
5. 對于一棵完全二叉樹,若從上至下、從左至右編號,則編號為 i 的節點,(葉節點除外)其左子節點的編號必為2i,(葉節點除外)其右子節點的編號必為 2i+1,(根節點除外)其父節點的編號必為i/2(取整除)。
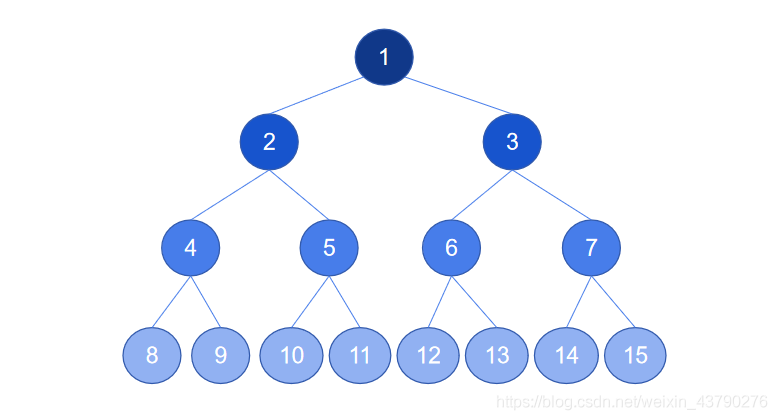
如下圖,這是一棵完全二叉樹,已經按規則編好號了,可以任意取一個節點進行驗證,都是符合此性質的。
到此這篇關于二叉樹的概念案例詳解的文章就介紹到這了,更多相關二叉樹的概念內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家!
您可能感興趣的文章:- Python rindex()方法案例詳解
- Python 實現靜態鏈表案例詳解
- Python 概率生成問題案例詳解
- Python實現堆排序案例詳解
- python讀取mnist數據集方法案例詳解
- 超實用的 10 段 Python 案例