項目介紹
背景：
DC競賽比賽項目，運用回歸模型進行房價預測。
數(shù)據(jù)介紹：
數(shù)據(jù)主要包括2014年5月至2015年5月美國King County的房屋銷售價格以及房屋的基本信息。
其中訓練數(shù)據(jù)主要包括10000條記錄，14個字段，分別代表：
- 銷售日期（date）：2014年5月到2015年5月房屋出售時的日期；
- 銷售價格（price）：房屋交易價格，單位為美元，是目標預測值；
- 臥室數(shù)（bedroom_num）：房屋中的臥室數(shù)目；
- 浴室數(shù)（bathroom_num）:房屋中的浴室數(shù)目；
- 房屋面積（house_area）：房屋里的生活面積；
- 停車面積（park_space）：停車坪的面積；
- 樓層數(shù)（floor_num）：房屋的樓層數(shù)；
- 房屋評分（house_score）：King County房屋評分系統(tǒng)對房屋的總體評分；
- 建筑面積（covered_area）：除了地下室之外的房屋建筑面積；
- 地下室面積（basement_area）：地下室的面積；
- 建筑年份（yearbuilt）：房屋建成的年份；
- 修復年份（yearremodadd）：房屋上次修復的年份；
- 緯度（lat）：房屋所在緯度；
- 經(jīng)度（long）：房屋所在經(jīng)度。
目標：
算法通過計算平均預測誤差來衡量回歸模型的優(yōu)劣。平均預測誤差越小，說明回歸模型越好。
代碼詳解
數(shù)據(jù)導入
先導入分析需要的python包：
#導入類庫和加載數(shù)據(jù)集
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
導入下載好的kc_train的csv文件：
#讀取數(shù)據(jù)
train_names = ["date",
"price",
"bedroom_num",
"bathroom_num",
"house_area",
"park_space",
"floor_num",
"house_score",
"covered_area",
"basement_area",
"yearbuilt",
"yearremodadd",
"lat",
"long"]
data = pd.read_csv("kc_train.csv",names=train_names)
data.head()
數(shù)據(jù)預處理
查看數(shù)據(jù)集概況
# 觀察數(shù)據(jù)集概況
data.info()
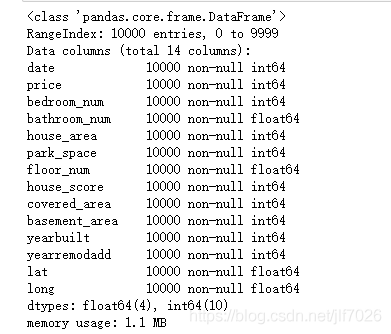
從圖中可以看出沒有任何缺失值，因此不需要對缺失值進行處理。
拆分數(shù)據(jù)：
把原始數(shù)據(jù)中的年月日拆開，然后根據(jù)房屋的建造年份和修復年份計算一下售出時已經(jīng)過了多少年，這樣就有17個特征。
sell_year,sell_month,sell_day=[],[],[]
house_old,fix_old=[],[]
for [date,yearbuilt,yearremodadd] in data[['date','yearbuilt','yearremodadd']].values:
year,month,day=date//10000,date%10000//100,date%100
sell_year.append(year)
sell_month.append(month)
sell_day.append(day)
house_old.append(year-yearbuilt)
if yearremodadd==0:
fix_old.append(0)
else:
fix_old.append(year-yearremodadd)
del data['date']
data['sell_year']=pd.DataFrame({'sell_year':sell_year})
data['sell_month']=pd.DataFrame({'sell_month':sell_month})
data['sell_day']=pd.DataFrame({'sell_day':sell_day})
data['house_old']=pd.DataFrame({'house_old':house_old})
data['fix_old']=pd.DataFrame({'fix_old':fix_old})
data.head()
觀察因變量（price)數(shù)據(jù)情況
#觀察數(shù)據(jù)
print(data['price'].describe())
#觀察price的數(shù)據(jù)分布
plt.figure(figsize = (10,5))
# plt.xlabel('price')
sns.distplot(data['price'])
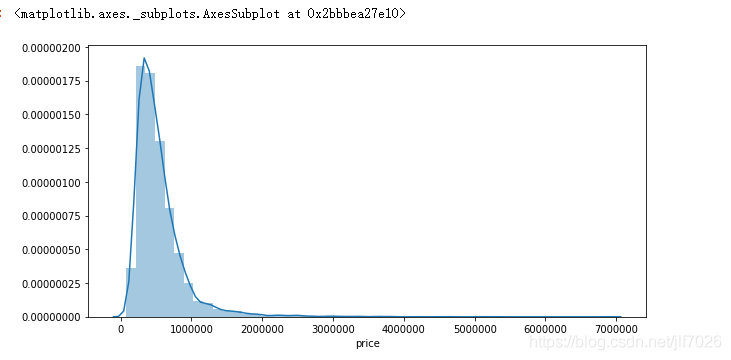
從數(shù)據(jù)和圖片上可以看出，price呈現(xiàn)典型的右偏分布，但總體上看還是符合一般規(guī)律。
相關性分析
自變量與因變量的相關性分析，繪制相關性矩陣熱力圖，比較各個變量之間的相關性：
#自變量與因變量的相關性分析
plt.figure(figsize = (20,10))
internal_chars = ['price','bedroom_num','bathroom_num','house_area','park_space','floor_num','house_score','covered_area'
,'basement_area','yearbuilt','yearremodadd','lat','long','sell_year','sell_month','sell_day',
'house_old','fix_old']
corrmat = data[internal_chars].corr() # 計算相關系數(shù)
sns.heatmap(corrmat, square=False, linewidths=.5, annot=True) #熱力圖
csdn.net/jlf7026/article/details/84630414
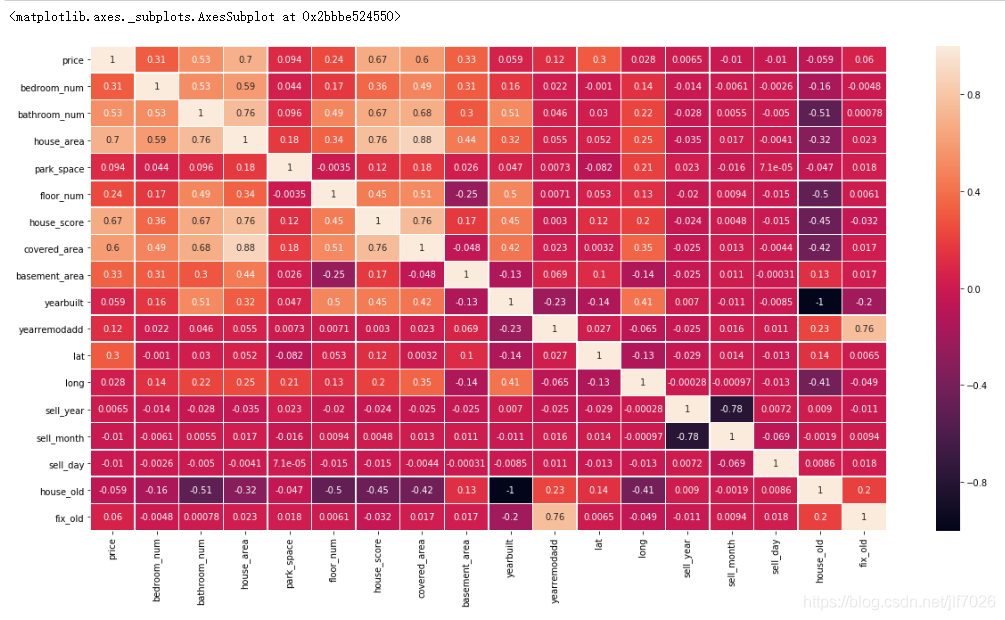
相關性越大，顏色越淺。看著可能不太清楚，因此看下排名
#打印出相關性的排名
print(corrmat["price"].sort_values(ascending=False))
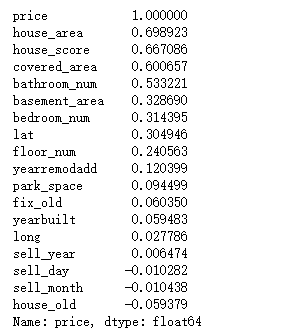
可以看出house_area,house_score,covered_area,bathroom_num這四個特征對price的影響最大，都超過了0.5。負數(shù)表明與price是負相關的。
特征選擇
一般來說，選擇一些與因變量（price）相關性比較大的做特征，但我嘗試過選擇前十的特征，然后進行建模預測，但得到的結果并不是很好，所以我還是把現(xiàn)有的特征全部用上。
歸一化
對于各個特征的數(shù)據(jù)范圍不一樣，影響線性回歸的效果，因此歸一化數(shù)據(jù)。
#特征縮放
data = data.astype('float')
x = data.drop('price',axis=1)
y = data['price']
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
newX= scaler.fit_transform(x)
newX = pd.DataFrame(newX, columns=x.columns)
newX.head()
劃分數(shù)據(jù)集
#先將數(shù)據(jù)集分成訓練集和測試集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(newX, y, test_size=0.2, random_state=21)
建立模型
選擇兩個模型進行預測，觀察那個模型更好。
#模型建立
from sklearn import metrics
def RF(X_train, X_test, y_train, y_test): #隨機森林
from sklearn.ensemble import RandomForestRegressor
model= RandomForestRegressor(n_estimators=200,max_features=None)
model.fit(X_train, y_train)
predicted= model.predict(X_test)
mse = metrics.mean_squared_error(y_test,predicted)
return (mse/10000)
def LR(X_train, X_test, y_train, y_test): #線性回歸
from sklearn.linear_model import LinearRegression
LR = LinearRegression()
LR.fit(X_train, y_train)
predicted = LR.predict(X_test)
mse = metrics.mean_squared_error(y_test,predicted)
return (mse/10000)
評價標準
算法通過計算平均預測誤差來衡量回歸模型的優(yōu)劣。平均預測誤差越小，說明回歸模型越好。
print('RF mse: ',RF(X_train, X_test, y_train, y_test))
print('LR mse: ',LR(X_train, X_test, y_train, y_test))
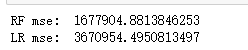
可以看出，隨機森林算法比線性回歸算法要好很多。
總結
對機器學習有了初步了解。但對于數(shù)據(jù)的預處理，和參數(shù)，特征，模型的調優(yōu)還很欠缺。
希望通過以后的學習，能不斷提高。也希望看這篇文章的朋友和我一起感受機器學習的魅力，更多相關機器學習內容請搜索腳本之家以前的文章或繼續(xù)瀏覽下面的相關文章，希望大家以后多多支持腳本之家！
您可能感興趣的文章:- 如何用Python進行時間序列分解和預測
- 利用keras使用神經(jīng)網(wǎng)絡預測銷量操作
- 詳解用Python進行時間序列預測的7種方法
- Python實現(xiàn)新型冠狀病毒傳播模型及預測代碼實例
- Datawhale練習之二手車價格預測
