昨晚被一則新聞刷屏:北京時間 4 月 10 日今晚 9 點,人類首張黑洞照片正式發布。
看到這張圖片,小吳心里是極為震撼的:愛因斯坦太太太太太牛逼了!!!
同時,看新聞的時候小吳還注意到里面有個細節,給黑洞”拍照“的事件視界望遠鏡從 2017 年就開始為黑洞拍照了,但直到 2019 年才公布。
心里不禁納悶:為什么給黑洞拍照需要這么長時間?
于是去更加詳細的搜索資料,果然發現了端倪,其中一個點就是 望遠鏡觀測到的數據量非常龐大 !
2017 年時 8 個望遠鏡的數據量達到了 10PB(=10240TB),2018 年又增加了格陵蘭島望遠鏡,數據量繼續增加。龐大的數據量為處理讓數據處理的難度不斷加大。
平時面試的時候老是說海量數據,海量數據,這次的數據真的是海量數據了。
這次的數據流之大,導致每個射電望遠鏡產生的數據,都只能用硬盤來儲存。
那么現在問題來了,假設你作為給黑洞拍照的研發人員,給你一臺內存有限的計算機,你如何找出這些數據的中位數或者判斷某個數字是否存在里面。
1. 海量數據查找中位數
題目描述
現在有 10 億個 int 型的數字( java 中 int 型占 4B),以及一臺可用內存為 1GB 的機器,如何找出這 10 億個數字的中位數?
所謂中位數就是有序列表中間的數。如果列表長度是偶數,中位數則是中間兩個數的平均值。
題目解析
題目中有 10 億個數字,每個數字在內存中占 4B,那么這 10 億個數字完全加載到內存中需要:10 * 10^8 * 4,大概需要 4GB 的存儲空間。根據題目的限制,顯然不能把所有的數字都裝入內存中。
這里,可以采用基于 二進制位比較 和 快速排序算法中的 分割思想 來尋找中位數,實際上這也是 桶排序 的一種應用。
 桶排序
桶排序
假設將這 10 億個數字保存在一個大文件中,依次讀一部分文件到內存(不超過內存的限制: 1GB ),將每個數字用二進制表示,比較二進制的最高位(第 32 位),如果數字的最高位為 0,則將這個數字寫入 file_0 文件中;如果最高位為 1,則將該數字寫入 file_1 文件中。
注意:最高位為符號位,也就是說 file_1 中的數都是負數,而 file_0 中的數都是正數。
通過這樣的操作,這 10 億個數字分成了兩個文件,假設 file_0 文件中有 6 億個數字,而 file_1 文件中有 4 億個數字。
這樣劃分后,思考一下:所求的中位數在哪個文件中?
10 億個數字的中位數是10 億個數排序之后的第 5 億個數,現在 file_0 有 6 億個正數,file_1 有 4 億個負數,file_0 中的數都比 file_1 中的數要大,排序之后的第 5 億個數一定是正數,那么排序之后的第 5 億個數一定位于file_0中。
也就是說:中位數就在 file_0 文件中,并且是 file_0 文件中所有數字排序之后的第 1 億個數字。
現在,我們只需要處理 file_0 文件了(不需要再考慮 file_1 文件)。
而對于 file_0 文件,可以同樣的采取上面的措施處理:將 file_0 文件依次讀一部分到內存(不超內存限制:1GB ),將每個數字用二進制表示,比較二進制的 次高位(第 31 位),如果數字的次高位為 0,寫入 file_0_0 文件中;如果次高位為 1 ,寫入 file_0_1 文件中。
現假設 file_0_0 文件中有 3 億個數字,file_0_1中也有 3 億個數字,則中位數就是:file_0_0 文件中的數字從小到大排序之后的第 1 億個數字。
拋棄 file_0_1 文件,繼續對 file_0_0 文件 根據次次高位(第 30 位) 劃分,假設此次劃分的兩個文件為:file_0_0_0中有 0.5 億個數字,file_0_0_1 中有 2.5 億個數字,那么中位數就是 file_0_0_1 文件中的所有數字排序之后的第 0.5 億個數。
2. 海量數據中判斷數字是否存在
題目描述
現在有 10 億個 int 型的數字( java 中 int 型占 4B),以及一臺可用內存為 1GB 的機器,給出一個整數,問如果快速地判斷這個整數是否在這 10 億數字中?
題目分析
這里可以使用 布隆過濾器 進行處理。
布隆過濾器(英語:Bloom Filter)是 1970 年由 Burton Bloom 提出的。
它實際上是一個很長的二進制矢量和一系列隨機映射函數。
它可以用來判斷一個元素是否在一個集合中。它的優勢是只需要占用很小的內存空間以及有著高效的查詢效率。
對于布隆過濾器而言,它的本質是一個位數組:位數組就是數組的每個元素都只占用 1 bit ,并且每個元素只能是 0 或者 1。
一開始,布隆過濾器的位數組所有位都初始化為 0。比如,數組長度為 m ,那么將長度為 m 個位數組的所有的位都初始化為 0。
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
。 |
。 |
。 |
。 |
。 |
m-2 |
m-1 |
|
在數組中的每一位都是二進制位。
布隆過濾器除了一個位數組,還有 K 個哈希函數。當一個元素加入布隆過濾器中的時候,會進行如下操作:
使用 K 個哈希函數對元素值進行 K 次計算,得到 K 個哈希值。根據得到的哈希值,在位數組中把對應下標的值置為 1。
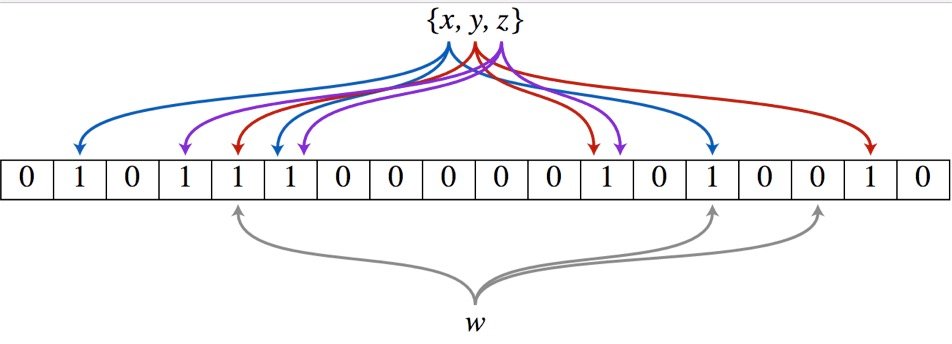 圖 1
圖 1
舉個例子,假設布隆過濾器有 3 個哈希函數:f1, f2, f3 和一個位數組 arr。現在要把 2333 插入布隆過濾器中:
對值進行三次哈希計算,得到三個值 n1, n2, n3。把位數組中三個元素 arr[n1], arr[n2], arr[3] 都置為 1。
當要判斷一個值是否在布隆過濾器中,對元素進行三次哈希計算,得到值之后判斷位數組中的每個元素是否都為 1,如果值都為 1,那么說明這個值在布隆過濾器中,如果存在一個值不為 1,說明該元素不在布隆過濾器中。
 布隆
布隆
總結
以上所述是小編給大家介紹的幾道和「黑洞照片」那種海量數據有關的算法問題,希望對大家有所幫助,如果大家有任何疑問請給我留言,小編會及時回復大家的。在此也非常感謝大家對腳本之家網站的支持!
如果你覺得本文對你有幫助,歡迎轉載,煩請注明出處,謝謝!
您可能感興趣的文章:- Python數據結構與算法之圖的最短路徑(Dijkstra算法)完整實例
- JS實現的數組去除重復數據算法小結
- Python數據結構與算法之圖結構(Graph)實例分析
- C++數據結構與算法之雙緩存隊列實現方法詳解
 圖 1
圖 1 布隆
布隆