目錄
- 1.數據分離與驗證
- 1.1分離訓練數據集和評估數據集
- 1.2K折交叉驗證分離
- 1.3棄一交叉驗證分離
- 1.4重復隨機分離評估數據集與訓練數據集
- 2.算法評估
- 2.1分類算法評估
- 2.2回歸算法評估
- 2.2.1平均絕對誤差
- 2.2.2均方誤差
- 2.2.3判定系數(
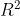 )
)
1.數據分離與驗證
要知道算法模型對未知的數據表現如何,最好的評估辦法是利用已經明確知道結果的數據運行生成的算法模型進行驗證。此外還可以使用新的數據來評估算法模型。
在評估機器學習算法時,不將訓練集直接作為評估數據集最直接的原因就是過度擬合。過度擬合是指為了得到一致性假設而變得過度嚴格,簡單來說就是指模型僅對訓練數據有較好的效果,而對于新數據則適應性很差。
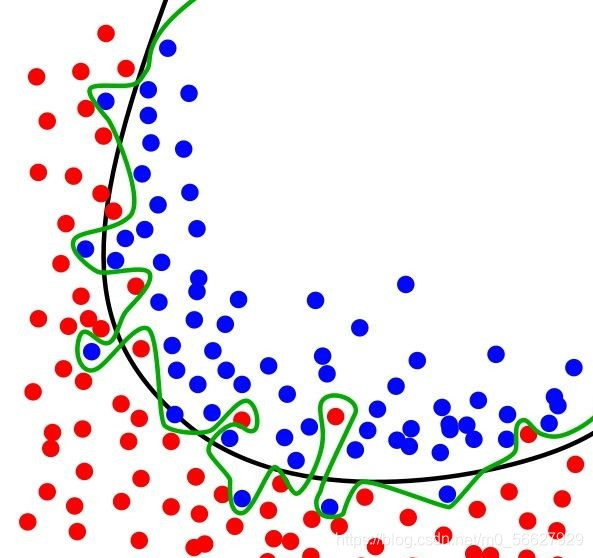
如圖所示是一個分類實例,綠色曲線表示過擬合,黑色曲線表示正常模型。可以看到過擬合模型僅對當前數據表現較好,而對新數據適應性明顯不如正常模型。
接下來將講解四種不同的分離數據集的方法,用來分離訓練集和評估集,并用其評估算法模型。
1.1分離訓練數據集和評估數據集
可以簡單地將原始數據集分為兩部分,第一部分用來訓練算法生成模型,第二部分通過模型來預測結果,并于已知的結果進行比較,來評估算法模型的準確度。
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import ShuffleSplit
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)
# print(data.head(10))
array = data.values
X = array[:, 0:8]
Y = array[:, 8]
test_size = 0.33
seed = 4
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
model = LogisticRegression(max_iter=3000)
model.fit(X_train, Y_train)
result = model.score(X_test, Y_test)
print("算法評估結果:%3f%%" % (result * 100))
執行后得到的結果約為80%。為了讓算法模型具有良好的可復用性,在指定了分離數據大小的同時,還指定了隨機粒度(seed=4),將數據隨即進行分離。通過指定隨機的粒度,可以確保每次執行程序得到相同的結果,這有助于比較兩個不同的算法生成模型的結果。
算法評估結果:80.314961%
1.2K折交叉驗證分離
K折交叉驗證是將原始數據分成K組(一般是均分),將第一部分作為測試集,其余作為訓練集,訓練模型,計算模型在測試集上的準確率,每次用不同部分作為測試集,重復上述步驟K次,最后將平均準確率作為最終的模型準確率。
# K折交叉驗證分離
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds, random_state=seed,shuffle=True)
model = LogisticRegression(max_iter=3000)
result = cross_val_score(model, X, Y, cv=kfold)
print("算法評估結果:%.3f%% (%.3f%%)" % (result.mean() * 100, result.std() * 100))
執行后得到評估得分及標準方差。
算法評估結果:77.216% (4.968%)
1.3棄一交叉驗證分離
相較于K折交叉驗證分離,棄一交叉驗證有顯著優點:
- 每一回合中幾乎所有樣本你皆用于訓練模型,因此最接近原始樣本的分布,這樣評估所得的結果比較可靠。
- 實驗過程中沒有隨機因素會影響實驗數據,確保實驗過程可重復。
但棄一交叉驗證計算成本高,當原始數據樣本數量多時,棄一交叉驗證需要花費大量時間完成評估。
# 棄一交叉驗證分離
# 計算量非常大!!
loocv = LeaveOneOut()
model = LogisticRegression(max_iter=3000)
result = cross_val_score(model,X,Y,cv = loocv)
print("算法評估結果:%.3f%% (%.3f%%)"% (result.mean()*100,result.std()*100))
運算得出的標準方差與K折交叉驗證有較大差距。
算法評估結果:77.604% (41.689%)
1.4重復隨機分離評估數據集與訓練數據集
另外一種K折交叉驗證的用途是隨即分離數據為訓練數據集和評估數據集。
n_splits = 10
test_size = 0.33
seed = 7
kfold = ShuffleSplit(n_splits=n_splits, test_size=test_size, random_state=seed)
model = LogisticRegression(max_iter=3000)
result = cross_val_score(model, X, Y, cv=kfold)
print("算法評估結果:%.3f%% (%.3f%%)" % (result.mean() * 100, result.std() * 100))
算法評估結果:76.535% (2.235%)
2.算法評估
2.1分類算法評估
2.1.1分類準確度
分類準確度就是算法自動分類正確的樣本數除以所有的樣本數得出的結果。準確度是一個很好、很直觀的評價指標,但是有時候準確度高并不代表算法就一定好。
from pandas import read_csv
import pandas as pd
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
#分類準確度
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename,names=names)
#print(data.head(10))
#將數據分為輸入數據和輸出結果
array = data.values
X = array[:,0:8]
Y = array[:,8]
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
model = LogisticRegression(max_iter=3000)
result = cross_val_score(model, X,Y,cv=kfold)
print("算法評估結果準確度:%.3f(%.3f)" % (result.mean(),result.std()))
算法評估結果準確度:0.772(0.050)
2.1.2分類報告
在scikit-learn中提供了一個非常方便的工具,可以給出對分類問題的評估報告,Classification__report()方法能夠給出precision,recall,F1-score,support。
from pandas import read_csv
import pandas as pd
from sklearn.model_selection import KFold
from sklearn.metrics import classification_report
#分類準確度
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename,names=names)
print(data.head(10))
#將數據分為輸入數據和輸出結果
array = data.values
X = array[:,0:8]
Y = array[:,8]
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
model = LogisticRegression(max_iter=3000)
model.fit(X_train,Y_train)
predicted = model.predict(X_test)
report = classification_report(Y_test, predicted)
print(report)
precision recall f1-score support
0.0 0.84 0.87 0.86 171
1.0 0.71 0.66 0.69 83
accuracy 0.80 254
macro avg 0.78 0.77 0.77 254
weighted avg 0.80 0.80 0.80 254
2.2回歸算法評估
回歸算法評估將使用波士頓房價(Boston House Price)數據集。可通過百度網盤下載
鏈接:https://pan.baidu.com/s/1uyDiXDC-ixfBIYmTU9rrAQ
提取碼:eplz
2.2.1平均絕對誤差
平均絕對誤差是所有單個觀測值與算術平均值偏差絕對值的平均值。平均絕對誤差相比于平均誤差能更好地反映預測值誤差的實際情況。
cross_val_score中的scoring參數詳解可見官方開發文檔
https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
filename = 'housing.csv'
names = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PRTATIO','B','LSTAT','MEDV']
data = read_csv(filename,names=names,delim_whitespace=True)
array = data.values
X = array[:,0:13]
Y = array[:,13]
n_splits = 10
seed = 7
kfold = KFold(n_splits=n_splits,random_state=seed,shuffle=True)
model = LinearRegression()
#平均絕對誤差
scoring = 'neg_mean_absolute_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print('MAE:%.3f(%.3f)'% (result.mean(),result.std()))
MAE:-3.387(0.667)
2.2.2均方誤差
均方誤差是衡量平均誤差的方法,可以評價數據的變化程度。均方根誤差是均方誤差的算術平均跟。均方誤差越小,說明用該預測模型描述實驗數據準確度越高。
#均方誤差
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print('MSE:%.3f(%.3f)'% (result.mean(),result.std()))
MSE:-23.747(11.143)
2.2.3判定系數(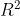 )
)
判定系數(coefficient of determination),也叫可決系數或決定系數,是指在線性回歸中,回歸平方和與總離差平方和之比值,其數值等于相關系數的平方。
#決定系數
scoring = 'r2'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print('R2:%.3f(%.3f)'% (result.mean(),result.std()))
R2:0.718(0.099)
K折交叉驗證是用來評估機器學習算法的黃金準則。黃金準則為:當不知如何選擇分離數據集的方法時,選擇K折交叉驗證來分離數據集;當不知如何設定K值時,將K設為10。
到此這篇關于Python機器學習入門(四)選擇模型的文章就介紹到這了,更多相關Python機器學習內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家!
您可能感興趣的文章:- Python機器學習入門(一)序章
- Python機器學習入門(二)之Python數據理解
- Python機器學習入門(三)之Python數據準備
- Python機器學習入門(五)之Python算法審查
- Python機器學習入門(六)之Python優化模型
- python機器學習高數篇之函數極限與導數