目錄
- 一、技術(shù)背景
- 二、MindSpore內(nèi)置的損失函數(shù)
- 三、自定義損失函數(shù)
- 四、自定義其他算子
- 五、多層算子的應(yīng)用
- 六、重定義reduction
一、技術(shù)背景
損失函數(shù)是機(jī)器學(xué)習(xí)中直接決定訓(xùn)練結(jié)果好壞的一個(gè)模塊，該函數(shù)用于定義計(jì)算出來(lái)的結(jié)果或者是神經(jīng)網(wǎng)絡(luò)給出的推測(cè)結(jié)論與正確結(jié)果的偏差程度，偏差的越多，就表明對(duì)應(yīng)的參數(shù)越差。而損失函數(shù)的另一個(gè)重要性在于會(huì)影響到優(yōu)化函數(shù)的收斂性，如果損失函數(shù)的指數(shù)定義的太高，稍有參數(shù)波動(dòng)就導(dǎo)致結(jié)果的巨大波動(dòng)的話，那么訓(xùn)練和優(yōu)化就很難收斂。一般我們常用的損失函數(shù)是MSE（均方誤差）和MAE（平均標(biāo)準(zhǔn)差）等。那么這里我們嘗試在MindSpore中去自定義一些損失函數(shù)，可用于適應(yīng)自己的特殊場(chǎng)景。
二、MindSpore內(nèi)置的損失函數(shù)
剛才提到的MSE和MAE等常見(jiàn)損失函數(shù)，MindSpore中是有內(nèi)置的，通過(guò)net_loss = nn.loss.MSELoss()即可調(diào)用，再傳入Model中進(jìn)行訓(xùn)練，具體使用方法可以參考如下擬合一個(gè)非線性函數(shù)的案例：
# test_nonlinear.py
from mindspore import context
import numpy as np
from mindspore import dataset as ds
from mindspore import nn, Tensor, Model
import time
from mindspore.train.callback import Callback, LossMonitor
import mindspore as ms
ms.common.set_seed(0)
def get_data(num, a=2.0, b=3.0, c=5.0):
for _ in range(num):
x = np.random.uniform(-1.0, 1.0)
y = np.random.uniform(-1.0, 1.0)
noise = np.random.normal(0, 0.03)
z = a * x ** 2 + b * y ** 3 + c + noise
yield np.array([[x**2], [y**3]],dtype=np.float32).reshape(1,2), np.array([z]).astype(np.float32)
def create_dataset(num_data, batch_size=16, repeat_size=1):
input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['xy','z'])
input_data = input_data.batch(batch_size)
input_data = input_data.repeat(repeat_size)
return input_data
data_number = 160
batch_number = 10
repeat_number = 10
ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)
class LinearNet(nn.Cell):
def __init__(self):
super(LinearNet, self).__init__()
self.fc = nn.Dense(2, 1, 0.02, 0.02)
def construct(self, x):
x = self.fc(x)
return x
start_time = time.time()
net = LinearNet()
model_params = net.trainable_params()
print ('Param Shape is: {}'.format(len(model_params)))
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
net_loss = nn.loss.MSELoss()
optim = nn.Momentum(net.trainable_params(), learning_rate=0.01, momentum=0.6)
model = Model(net, net_loss, optim)
epoch = 1
model.train(epoch, ds_train, callbacks=[LossMonitor(10)], dataset_sink_mode=True)
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
print ('The total time cost is: {}s'.format(time.time() - start_time))
訓(xùn)練的結(jié)果如下：
epoch: 1 step: 160, loss is 2.5267093
Parameter (name=fc.weight, shape=(1, 2), dtype=Float32, requires_grad=True) [[1.0694231 0.12706374]]
Parameter (name=fc.bias, shape=(1,), dtype=Float32, requires_grad=True) [5.186701]
The total time cost is: 8.412306308746338s
最終優(yōu)化出來(lái)的loss值是2.5，不過(guò)在損失函數(shù)定義不同的情況下，單純只看loss值是沒(méi)有意義的。所以通常是大家統(tǒng)一定一個(gè)測(cè)試的標(biāo)準(zhǔn)，比如大家都用MAE來(lái)衡量最終訓(xùn)練出來(lái)的模型的好壞，但是中間訓(xùn)練的過(guò)程不一定采用MAE來(lái)作為損失函數(shù)。
三、自定義損失函數(shù)
由于python語(yǔ)言的靈活性，使得我們可以繼承基本類(lèi)和函數(shù)，只要使用mindspore允許范圍內(nèi)的算子，就可以實(shí)現(xiàn)自定義的損失函數(shù)。我們先看一個(gè)簡(jiǎn)單的案例，暫時(shí)將我們自定義的損失函數(shù)命名為L(zhǎng)1Loss：
# test_nonlinear.py
from mindspore import context
import numpy as np
from mindspore import dataset as ds
from mindspore import nn, Tensor, Model
import time
from mindspore.train.callback import Callback, LossMonitor
import mindspore as ms
import mindspore.ops as ops
from mindspore.nn.loss.loss import Loss
ms.common.set_seed(0)
def get_data(num, a=2.0, b=3.0, c=5.0):
for _ in range(num):
x = np.random.uniform(-1.0, 1.0)
y = np.random.uniform(-1.0, 1.0)
noise = np.random.normal(0, 0.03)
z = a * x ** 2 + b * y ** 3 + c + noise
yield np.array([[x**2], [y**3]],dtype=np.float32).reshape(1,2), np.array([z]).astype(np.float32)
def create_dataset(num_data, batch_size=16, repeat_size=1):
input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['xy','z'])
input_data = input_data.batch(batch_size)
input_data = input_data.repeat(repeat_size)
return input_data
data_number = 160
batch_number = 10
repeat_number = 10
ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)
class LinearNet(nn.Cell):
def __init__(self):
super(LinearNet, self).__init__()
self.fc = nn.Dense(2, 1, 0.02, 0.02)
def construct(self, x):
x = self.fc(x)
return x
start_time = time.time()
net = LinearNet()
model_params = net.trainable_params()
print ('Param Shape is: {}'.format(len(model_params)))
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
class L1Loss(Loss):
def __init__(self, reduction="mean"):
super(L1Loss, self).__init__(reduction)
self.abs = ops.Abs()
def construct(self, base, target):
x = self.abs(base - target)
return self.get_loss(x)
user_loss = L1Loss()
optim = nn.Momentum(net.trainable_params(), learning_rate=0.01, momentum=0.6)
model = Model(net, user_loss, optim)
epoch = 1
model.train(epoch, ds_train, callbacks=[LossMonitor(10)], dataset_sink_mode=True)
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
print ('The total time cost is: {}s'.format(time.time() - start_time))
這里自己定義的內(nèi)容實(shí)際上有兩個(gè)部分，一個(gè)是construct函數(shù)中的計(jì)算結(jié)果的函數(shù)，比如這里使用的是求絕對(duì)值。另外一個(gè)定義的部分是reduction參數(shù)，我們從mindspore的源碼中可以看到，這個(gè)reduction函數(shù)可以決定調(diào)用哪一種計(jì)算方法，定義好的有平均值、求和、保持不變?nèi)N策略。
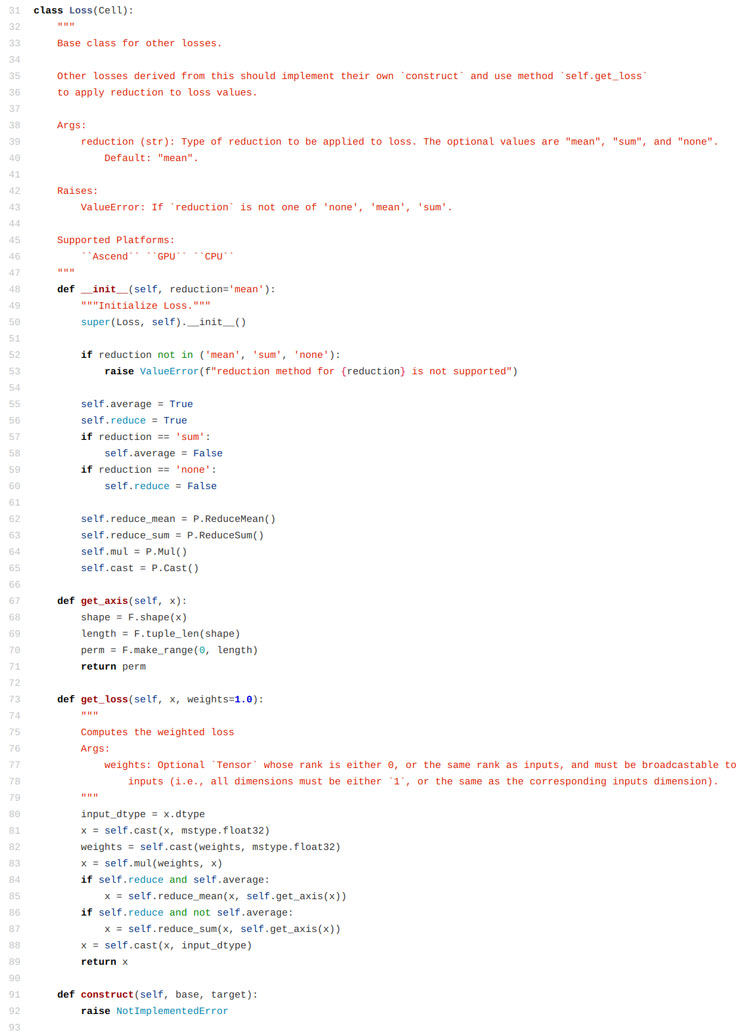
那么最后看下自定義的這個(gè)損失函數(shù)的運(yùn)行結(jié)果：
epoch: 1 step: 160, loss is 1.8300734
Parameter (name=fc.weight, shape=(1, 2), dtype=Float32, requires_grad=True) [[ 1.2687287 -0.09565887]]
Parameter (name=fc.bias, shape=(1,), dtype=Float32, requires_grad=True) [3.7297544]
The total time cost is: 7.0749146938323975s
這里不必太在乎loss的值，因?yàn)榍懊嬉蔡岬搅耍煌膿p失函數(shù)框架下，計(jì)算出來(lái)的值就是不一樣的，小一點(diǎn)大一點(diǎn)并沒(méi)有太大意義，最終還是需要大家統(tǒng)一一個(gè)標(biāo)準(zhǔn)才能夠進(jìn)行很好的衡量和對(duì)比。
四、自定義其他算子
這里我們僅僅是替換了一個(gè)abs的算子為square的算子，從求絕對(duì)值變化到求均方誤差，這里只是修改了一個(gè)算子，內(nèi)容較為簡(jiǎn)單：
# test_nonlinear.py
from mindspore import context
import numpy as np
from mindspore import dataset as ds
from mindspore import nn, Tensor, Model
import time
from mindspore.train.callback import Callback, LossMonitor
import mindspore as ms
import mindspore.ops as ops
from mindspore.nn.loss.loss import Loss
ms.common.set_seed(0)
def get_data(num, a=2.0, b=3.0, c=5.0):
for _ in range(num):
x = np.random.uniform(-1.0, 1.0)
y = np.random.uniform(-1.0, 1.0)
noise = np.random.normal(0, 0.03)
z = a * x ** 2 + b * y ** 3 + c + noise
yield np.array([[x**2], [y**3]],dtype=np.float32).reshape(1,2), np.array([z]).astype(np.float32)
def create_dataset(num_data, batch_size=16, repeat_size=1):
input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['xy','z'])
input_data = input_data.batch(batch_size)
input_data = input_data.repeat(repeat_size)
return input_data
data_number = 160
batch_number = 10
repeat_number = 10
ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)
class LinearNet(nn.Cell):
def __init__(self):
super(LinearNet, self).__init__()
self.fc = nn.Dense(2, 1, 0.02, 0.02)
def construct(self, x):
x = self.fc(x)
return x
start_time = time.time()
net = LinearNet()
model_params = net.trainable_params()
print ('Param Shape is: {}'.format(len(model_params)))
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
class L1Loss(Loss):
def __init__(self, reduction="mean"):
super(L1Loss, self).__init__(reduction)
self.square = ops.Square()
def construct(self, base, target):
x = self.square(base - target)
return self.get_loss(x)
user_loss = L1Loss()
optim = nn.Momentum(net.trainable_params(), learning_rate=0.01, momentum=0.6)
model = Model(net, user_loss, optim)
epoch = 1
model.train(epoch, ds_train, callbacks=[LossMonitor(10)], dataset_sink_mode=True)
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
print ('The total time cost is: {}s'.format(time.time() - start_time))
關(guān)于更多的算子內(nèi)容，可以參考下這個(gè)鏈接
(https://www.mindspore.cn/doc/api_python/zh-CN/r1.2/mindspore/mindspore.ops.html)中的內(nèi)容，
上述代碼的運(yùn)行結(jié)果如下：
epoch: 1 step: 160, loss is 2.5267093
Parameter (name=fc.weight, shape=(1, 2), dtype=Float32, requires_grad=True) [[1.0694231 0.12706374]]
Parameter (name=fc.bias, shape=(1,), dtype=Float32, requires_grad=True) [5.186701]
The total time cost is: 6.87545919418335s
可以從這個(gè)結(jié)果中發(fā)現(xiàn)的是，計(jì)算出來(lái)的結(jié)果跟最開(kāi)始使用的內(nèi)置的MSELoss結(jié)果是一樣的，這是因?yàn)槲覀冏远x的這個(gè)求損失函數(shù)的形式與內(nèi)置的MSE是吻合的。
五、多層算子的應(yīng)用
上面的兩個(gè)例子都是簡(jiǎn)單的說(shuō)明了一下通過(guò)單個(gè)算子構(gòu)造的損失函數(shù)，其實(shí)如果是一個(gè)復(fù)雜的損失函數(shù)，也可以通過(guò)多個(gè)算子的組合操作來(lái)進(jìn)行實(shí)現(xiàn)：
# test_nonlinear.py
from mindspore import context
import numpy as np
from mindspore import dataset as ds
from mindspore import nn, Tensor, Model
import time
from mindspore.train.callback import Callback, LossMonitor
import mindspore as ms
import mindspore.ops as ops
from mindspore.nn.loss.loss import Loss
ms.common.set_seed(0)
def get_data(num, a=2.0, b=3.0, c=5.0):
for _ in range(num):
x = np.random.uniform(-1.0, 1.0)
y = np.random.uniform(-1.0, 1.0)
noise = np.random.normal(0, 0.03)
z = a * x ** 2 + b * y ** 3 + c + noise
yield np.array([[x**2], [y**3]],dtype=np.float32).reshape(1,2), np.array([z]).astype(np.float32)
def create_dataset(num_data, batch_size=16, repeat_size=1):
input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['xy','z'])
input_data = input_data.batch(batch_size)
input_data = input_data.repeat(repeat_size)
return input_data
data_number = 160
batch_number = 10
repeat_number = 10
ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)
class LinearNet(nn.Cell):
def __init__(self):
super(LinearNet, self).__init__()
self.fc = nn.Dense(2, 1, 0.02, 0.02)
def construct(self, x):
x = self.fc(x)
return x
start_time = time.time()
net = LinearNet()
model_params = net.trainable_params()
print ('Param Shape is: {}'.format(len(model_params)))
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
class L1Loss(Loss):
def __init__(self, reduction="mean"):
super(L1Loss, self).__init__(reduction)
self.square = ops.Square()
def construct(self, base, target):
x = self.square(self.square(base - target))
return self.get_loss(x)
user_loss = L1Loss()
optim = nn.Momentum(net.trainable_params(), learning_rate=0.01, momentum=0.6)
model = Model(net, user_loss, optim)
epoch = 1
model.train(epoch, ds_train, callbacks=[LossMonitor(10)], dataset_sink_mode=True)
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
print ('The total time cost is: {}s'.format(time.time() - start_time))
這里使用的函數(shù)是兩個(gè)平方算子，也就是四次方的均方誤差，運(yùn)行結(jié)果如下：
epoch: 1 step: 160, loss is 16.992222
Parameter (name=fc.weight, shape=(1, 2), dtype=Float32, requires_grad=True) [[0.14460069 0.32045612]]
Parameter (name=fc.bias, shape=(1,), dtype=Float32, requires_grad=True) [5.6676607]
The total time cost is: 7.253541946411133s
在實(shí)際的運(yùn)算過(guò)程中，我們肯定不能夠說(shuō)提升損失函數(shù)的冪次就一定能夠提升結(jié)果的優(yōu)劣，但是通過(guò)多種基礎(chǔ)算子的組合，理論上說(shuō)我們?cè)谝欢ǖ恼`差允許范圍內(nèi)，是可以實(shí)現(xiàn)任意的一個(gè)損失函數(shù)（通過(guò)泰勒展開(kāi)取截?cái)囗?xiàng)）的。
六、重定義reduction
方才提到這里面自定義損失函數(shù)的兩個(gè)重點(diǎn)，一個(gè)是上面三個(gè)章節(jié)中所演示的construct函數(shù)的重寫(xiě)，這部分實(shí)際上是重新設(shè)計(jì)損失函數(shù)的函數(shù)表達(dá)式。另一個(gè)是reduction的自定義，這部分關(guān)系到不同的單點(diǎn)損失函數(shù)值之間的關(guān)系。舉個(gè)例子來(lái)說(shuō)，如果我們將reduction設(shè)置為求和，那么get_loss()這部分的函數(shù)內(nèi)容就是把所有的單點(diǎn)函數(shù)值加起來(lái)返回一個(gè)最終的值，求平均值也是類(lèi)似的。那么通過(guò)自定義一個(gè)新的get_loss()函數(shù)，我們就可以實(shí)現(xiàn)更加靈活的一些操作，比如我們可以選擇將所有的結(jié)果乘起來(lái)求積而不是求和（只是舉個(gè)例子，大部分情況下不會(huì)這么操作）。在python中要重寫(xiě)這個(gè)函數(shù)也容易，就是在繼承父類(lèi)的自定義類(lèi)中定義一個(gè)同名函數(shù)即可，但是注意我們最好是保留原函數(shù)中的一些內(nèi)容，在原內(nèi)容的基礎(chǔ)上加一些東西，冒然改模塊有可能導(dǎo)致不好定位的運(yùn)行報(bào)錯(cuò)。
# test_nonlinear.py
from mindspore import context
import numpy as np
from mindspore import dataset as ds
from mindspore import nn, Tensor, Model
import time
from mindspore.train.callback import Callback, LossMonitor
import mindspore as ms
import mindspore.ops as ops
from mindspore.nn.loss.loss import Loss
ms.common.set_seed(0)
def get_data(num, a=2.0, b=3.0, c=5.0):
for _ in range(num):
x = np.random.uniform(-1.0, 1.0)
y = np.random.uniform(-1.0, 1.0)
noise = np.random.normal(0, 0.03)
z = a * x ** 2 + b * y ** 3 + c + noise
yield np.array([[x**2], [y**3]],dtype=np.float32).reshape(1,2), np.array([z]).astype(np.float32)
def create_dataset(num_data, batch_size=16, repeat_size=1):
input_data = ds.GeneratorDataset(list(get_data(num_data)), column_names=['xy','z'])
input_data = input_data.batch(batch_size)
input_data = input_data.repeat(repeat_size)
return input_data
data_number = 160
batch_number = 10
repeat_number = 10
ds_train = create_dataset(data_number, batch_size=batch_number, repeat_size=repeat_number)
class LinearNet(nn.Cell):
def __init__(self):
super(LinearNet, self).__init__()
self.fc = nn.Dense(2, 1, 0.02, 0.02)
def construct(self, x):
x = self.fc(x)
return x
start_time = time.time()
net = LinearNet()
model_params = net.trainable_params()
print ('Param Shape is: {}'.format(len(model_params)))
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
class L1Loss(Loss):
def __init__(self, reduction="mean", config=True):
super(L1Loss, self).__init__(reduction)
self.square = ops.Square()
self.config = config
def construct(self, base, target):
x = self.square(base - target)
return self.get_loss(x)
def get_loss(self, x, weights=1.0):
print ('The data shape of x is: ', x.shape)
input_dtype = x.dtype
x = self.cast(x, ms.common.dtype.float32)
weights = self.cast(weights, ms.common.dtype.float32)
x = self.mul(weights, x)
if self.reduce and self.average:
x = self.reduce_mean(x, self.get_axis(x))
if self.reduce and not self.average:
x = self.reduce_sum(x, self.get_axis(x))
if self.config:
x = self.reduce_mean(x, self.get_axis(x))
weights = self.cast(-1.0, ms.common.dtype.float32)
x = self.mul(weights, x)
x = self.cast(x, input_dtype)
return x
user_loss = L1Loss()
optim = nn.Momentum(net.trainable_params(), learning_rate=0.01, momentum=0.6)
model = Model(net, user_loss, optim)
epoch = 1
model.train(epoch, ds_train, callbacks=[LossMonitor(10)], dataset_sink_mode=True)
for net_param in net.trainable_params():
print(net_param, net_param.asnumpy())
print ('The total time cost is: {}s'.format(time.time() - start_time))
上述代碼就是一個(gè)簡(jiǎn)單的案例，這里我們所做的操作，僅僅是把之前均方誤差的求和改成了求和之后取負(fù)數(shù)。還是需要再?gòu)?qiáng)調(diào)一遍的是，雖然我們定義的函數(shù)是非常簡(jiǎn)單的內(nèi)容，但是借用這個(gè)方法，我們可以更加靈活的去按照自己的設(shè)計(jì)定義一些定制化的損失函數(shù)。上述代碼的執(zhí)行結(jié)果如下：
The data shape of x is:
(10, 10, 1)
...
The data shape of x is:
(10, 10, 1)
epoch: 1 step: 160, loss is -310517200.0
Parameter (name=fc.weight, shape=(1, 2), dtype=Float32, requires_grad=True) [[-6154.176 667.4569]]
Parameter (name=fc.bias, shape=(1,), dtype=Float32, requires_grad=True) [-16418.32]
The total time cost is: 6.681089878082275s
一共打印了160個(gè)The data shape of x is...，這是因?yàn)槲覀冊(cè)趧澐州斎氲臄?shù)據(jù)集的時(shí)候，選擇了將160個(gè)數(shù)據(jù)劃分為每個(gè)batch含10個(gè)元素的模塊，那么一共就有16個(gè)batch，又對(duì)這16個(gè)batch重復(fù)10次，那么就是一共有160個(gè)batch，計(jì)算損失函數(shù)時(shí)是以batch為單位的，但是如果只是計(jì)算求和或者求平均值的話，不管劃分多少個(gè)batch結(jié)果都是一致的。
以上就是詳解MindSpore自定義模型損失函數(shù)的詳細(xì)內(nèi)容，更多關(guān)于MindSpore自定義模型損失函數(shù)的資料請(qǐng)關(guān)注腳本之家其它相關(guān)文章！
您可能感興趣的文章:- Python辦公自動(dòng)化之教你用Python批量識(shí)別發(fā)票并錄入到Excel表格中
- Python基礎(chǔ)之注釋的用法
- 在Linux下使用命令行安裝Python
