在看論文《Detecting Regions of Maximal Divergence for Spatio-Temporal Anomaly Detection》時,文中提到了這三種方法來比較時間序列中不同區(qū)域概率分布的差異。
KL散度、JS散度和交叉熵
三者都是用來衡量兩個概率分布之間的差異性的指標(biāo)。不同之處在于它們的數(shù)學(xué)表達(dá)。
對于概率分布P(x)和Q(x)
1)KL散度(Kullback–Leibler divergence)
又稱KL距離,相對熵。
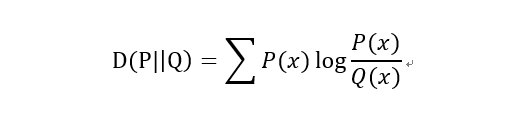
當(dāng)P(x)和Q(x)的相似度越高,KL散度越小。
KL散度主要有兩個性質(zhì):
(1)不對稱性
盡管KL散度從直觀上是個度量或距離函數(shù),但它并不是一個真正的度量或者距離,因為它不具有對稱性,即D(P||Q)!=D(Q||P)。
(2)非負(fù)性
相對熵的值是非負(fù)值,即D(P||Q)>0。
2)JS散度(Jensen-Shannon divergence)
JS散度也稱JS距離,是KL散度的一種變形。
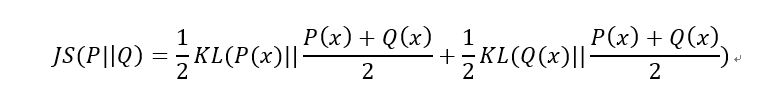
但是不同于KL主要又兩方面:
(1)值域范圍
JS散度的值域范圍是[0,1],相同則是0,相反為1。相較于KL,對相似度的判別更確切了。
(2)對稱性
即 JS(P||Q)=JS(Q||P),從數(shù)學(xué)表達(dá)式中就可以看出。
3)交叉熵(Cross Entropy)
在神經(jīng)網(wǎng)絡(luò)中,交叉熵可以作為損失函數(shù),因為它可以衡量P和Q的相似性。
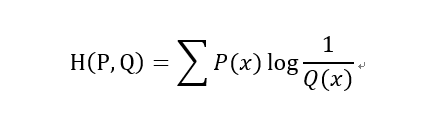
交叉熵和相對熵的關(guān)系:
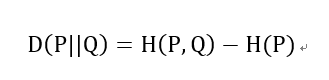
以上都是基于離散分布的概率,如果是連續(xù)的數(shù)據(jù),則需要對數(shù)據(jù)進(jìn)行Probability Density Estimate來確定數(shù)據(jù)的概率分布,就不是求和而是通過求積分的形式進(jìn)行計算了。
補(bǔ)充:信息熵、交叉熵與KL散度
信息量
在信息論與編碼中,信息量,也叫自信息(self-information),是指一個事件所能夠帶來信息的多少。一般地,這個事件發(fā)生的概率越小,其帶來的信息量越大。
從編碼的角度來看,這個事件發(fā)生的概率越大,其編碼長度越小,這個事件發(fā)生的概率越小,其編碼長度就越大。但是編碼長度小也是代價的,比如字母'a'用數(shù)字‘0'來表示時,為了避免歧義,就不能有其他任何以‘0'開頭的編碼了。
因此,信息量定義如下:
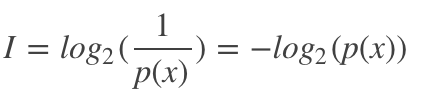
信息熵
信息熵是指一個概率分布p的平均信息量,代表著隨機(jī)變量或系統(tǒng)的不確定性,熵越大,隨機(jī)變量或系統(tǒng)的不確定性就越大。從編碼的角度來看,信息熵是表示一個概率分布p需要的平均編碼長度,其可表示為:
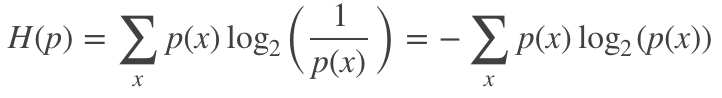
交叉熵
交叉熵是指在給定真實分布q情況下,采用一個猜測的分布p對其進(jìn)行編碼的平均編碼長度(或用猜測的分布來編碼真實分布得到的信息量)。
交叉熵可以用來衡量真實數(shù)據(jù)分布于當(dāng)前分布的相似性,當(dāng)前分布與真實分布相等時(q=p),交叉熵達(dá)到最小值。
其可定義為:
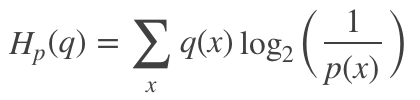
因此,在很多機(jī)器學(xué)習(xí)算法中都使用交叉熵作為損失函數(shù),交叉熵越小,當(dāng)前分布與真實分布越接近。此外,相比于均方誤差,交叉熵具有以下兩個優(yōu)點(diǎn):
在LR中,如果用均方誤差損失函數(shù),它是一個非凸函數(shù),而使用交叉熵?fù)p失函數(shù),它是一個凸函數(shù);
在LR中使用sigmoid激活函數(shù),如果使用均方誤差損失函數(shù),在對其求殘差時,其表達(dá)式與激活函數(shù)的導(dǎo)數(shù)有關(guān),而sigmoid(如下圖所示)的導(dǎo)數(shù)在輸入值超出[-5,5]范圍后將非常小,這會帶來梯度消失問題,而使用交叉熵?fù)p失函數(shù)則能避免這個問題。

KL散度
KL散度又稱相對熵,是衡量兩個分布之間的差異性。從編碼的角度來看,KL散度可表示為采用猜測分布p得到的平均編碼長度與采用真實分布q得到的平均編碼長度多出的bit數(shù),其數(shù)學(xué)表達(dá)式可定義為:
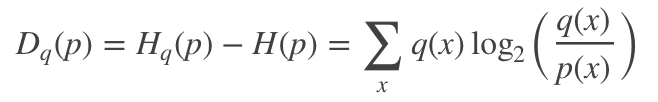
一般地,兩個分布越接近,其KL散度越小,最小為0.它具有兩個特性:
非負(fù)性,即KL散度最小值為0,其詳細(xì)證明可見[1] ;
非對稱性,即Dq(p)不等于Dp(q) ; KL散度與交叉熵之間的關(guān)系
在這里,再次盜用[1]的圖來形象地表達(dá)這兩者之間的關(guān)系:
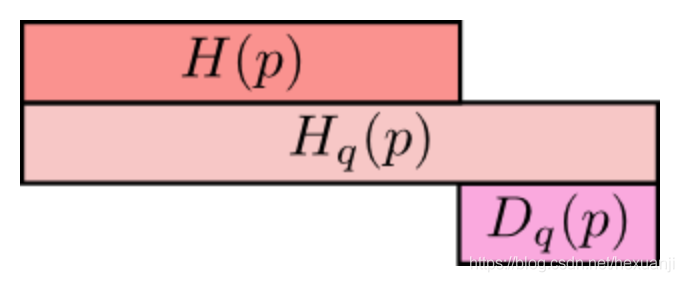
最上方cH(p)為信息熵,表示分布p的平均編碼長度/信息量;
中間的Hq(p)表示用分布q表編碼分布p所含的信息量或編碼長度,簡稱為交叉熵,其中Hq(p)>=H(p)
;最小方的Dq(p)表示的是q對p的KL距離,衡量了分布q和分布p之間的差異性,其中Dq(p)>=0;
從上圖可知,Hq(p) = H(p) + Dq(p)。
以上為個人經(jīng)驗,希望能給大家一個參考,也希望大家多多支持腳本之家。
您可能感興趣的文章:- pytorch 實現(xiàn)計算 kl散度 F.kl_div()
- Python 機(jī)器學(xué)習(xí)工具包SKlearn的安裝與使用
- python數(shù)據(jù)分析之用sklearn預(yù)測糖尿病
- pandas讀取excel,txt,csv,pkl文件等命令的操作
- python爬取之json、pickle與shelve庫的深入講解