基礎知識鋪墊

學習圖像金字塔，發現網上的資料比較多，檢索起來比較輕松。

圖像金字塔是一張圖像多尺度的表達，或者可以理解成一張圖像不同分辨率展示。

金字塔越底層的圖片，像素越高，越向上，像素逐步降低，分辨率逐步降低。

高斯金字塔

我們依舊不對概念做過多解釋，第一遍學習應用，應用，畢竟 365 天的周期，時間長，后面補充理論知識。

高斯金字塔用于向下采樣，同時它也是最基本的圖像塔。

在互聯網檢索原理，得到最簡單的說明如下：

將圖像的最底層（高斯金字塔的第 0 層），例如高斯核（5x5）對其進行卷積操作，這里的卷積主要處理掉的是偶數行與列，然后得到金字塔上一層圖像（即高斯金字塔第 1 層），在針對該圖像重復卷積操作，得到第 2 層，反復執行下去，即可得到高斯金字塔。

每次操作之后，都會將 M×N 圖像變成 M/2 × N/2 圖像，即減少一半。

還有實測中發現，需要用圖像的寬和高一致的圖片，并且寬高要是 2 的次冪數，例如，8 像素，16 像素，32 像素等等，一會你也可以實際測試一下。

圖像金字塔應用到的函數有 cv2.pyrDown() 和 cv2.pyrUp() 。

cv2.pyrDown 與 cv2.pyrUp 函數原型

通過 help 函數得到函數原型如下：

pyrDown(src[, dst[, dstsize[, borderType]]]) -> dst
pyrUp(src[, dst[, dstsize[, borderType]]]) -> dst

兩個函數原型參數一致，參數說明如下：

• src：輸入圖像；
• dst： 輸出圖像；
• dstsize： 輸出圖像尺寸，默認值按照 ((src.cols+1)/2, (src.rows+1)/2) 計算。

關于兩個函數的補充說明：

• cv2.pyrDown 從一個相對高分辨率的大尺寸的圖像上構建一個金字塔，運行之后的結果是，圖像變小，分辨率降低（下采樣）；
• cv2.pyrUp 是一個上采樣的過程，盡管相對尺寸變大，但是分辨率不會增加，圖像會變得更模糊。

測試代碼如下：

import cv2 as cv

src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采樣
dst = cv.pyrDown(src)
print(dst.shape[:2])
cv.imshow("dst", dst)

# 再次向下采樣
dst1 = cv.pyrDown(dst)
print(dst1.shape[:2])
cv.imshow("dst1", dst1)

cv.waitKey()

運行代碼之后，得到三張圖片，大小依次減小，分辨率降低。

通過上面運行得到的最小圖，在執行向上采樣之后，圖片會變的模糊，這也說明上采樣和下采樣是非線性處理，它們是不可逆的有損處理，因此下采樣后的圖像是無法還原的，即使放大圖片也會變模糊（后面學習到拉普拉斯金字塔可以解決該問題）。

# 向上采樣
dst2 = cv.pyrUp(dst1)
print(dst2.shape[:2])
cv.imshow("dst2", dst2)

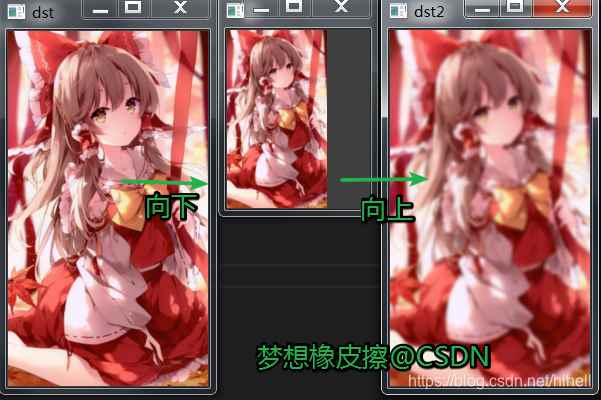
在總結一下上采樣和下采樣的步驟：

• 上采樣：使用 cv2.pyrUp 函數， 先將圖像在每個方向放大為原來的兩倍，新增的行和列用 0 填充，再使用先前同樣的內核與放大后的圖像卷積，獲得新增像素的近似值;
• 下采樣：使用 cv2.pyrDown 函數，先對圖像進行高斯內核卷積 ，再將所有偶數行和列去除。

拉普拉斯金字塔（Laplacian Pyramid， LP）

拉普拉斯金字塔主要用于重建圖像，由上文我們已經知道在使用高斯金字塔的的時候，上采樣和下采樣會導致圖像細節丟失。

拉普拉斯就是為了在放大圖像的時候，可以預測殘差，何為殘差，即小圖像放大的時候，需要插入一些像素值，在上文直接插入的是 0，拉普拉斯金字塔算法可以根據周圍像素進行預測，從而實現對圖像最大程度的還原。

學習到原理如下：用高斯金字塔的每一層圖像，減去其上一層圖像上采樣并高斯卷積之后的預測圖像，得到一系列的差值圖像即為 LP 分解圖像（其中 LP 即為拉普拉斯金字塔圖像）。

關于拉普拉斯還存在一個公式（這是本系列課程第一次書寫公式），其中 L 為拉普拉斯金字塔圖像，G 為高斯金字塔圖像

使用下面的代碼進行測試。

import cv2 as cv

src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采樣一次
dst = cv.pyrDown(src)
print(dst.shape[:2])
cv.imshow("dst", dst)

# 向上采樣一次
dst1 = cv.pyrUp(dst)
print(dst1.shape[:2])
cv.imshow("dst1", dst1)

# 計算拉普拉斯金字塔圖像
# 原圖 - 向上采樣一次的圖
laplace = cv.subtract(src, dst1)
cv.imshow("laplace", laplace)
cv.waitKey()

運行結果如下，相關的圖像已經呈現出來，重點注意最右側的圖片。

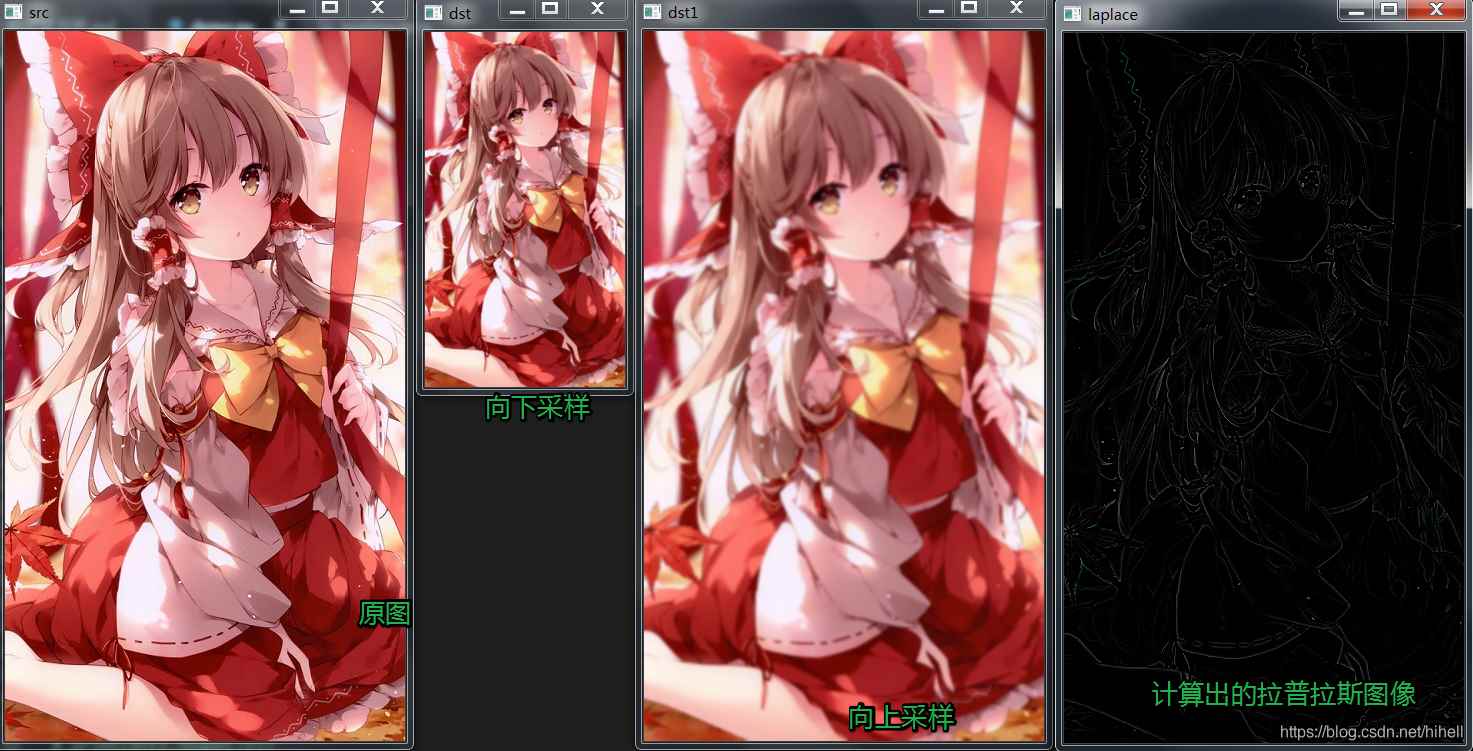
這個地方需要注意下，如果你使用 cv.subtract(src, dst1) 函數，得到的是上圖效果，但是在使用還原的時候會發現問題，建議直接使用 -完成，匹配公式，修改代碼如下：

# cv.subtract(src, dst1)
laplace = src - dst1

代碼運行效果如下。

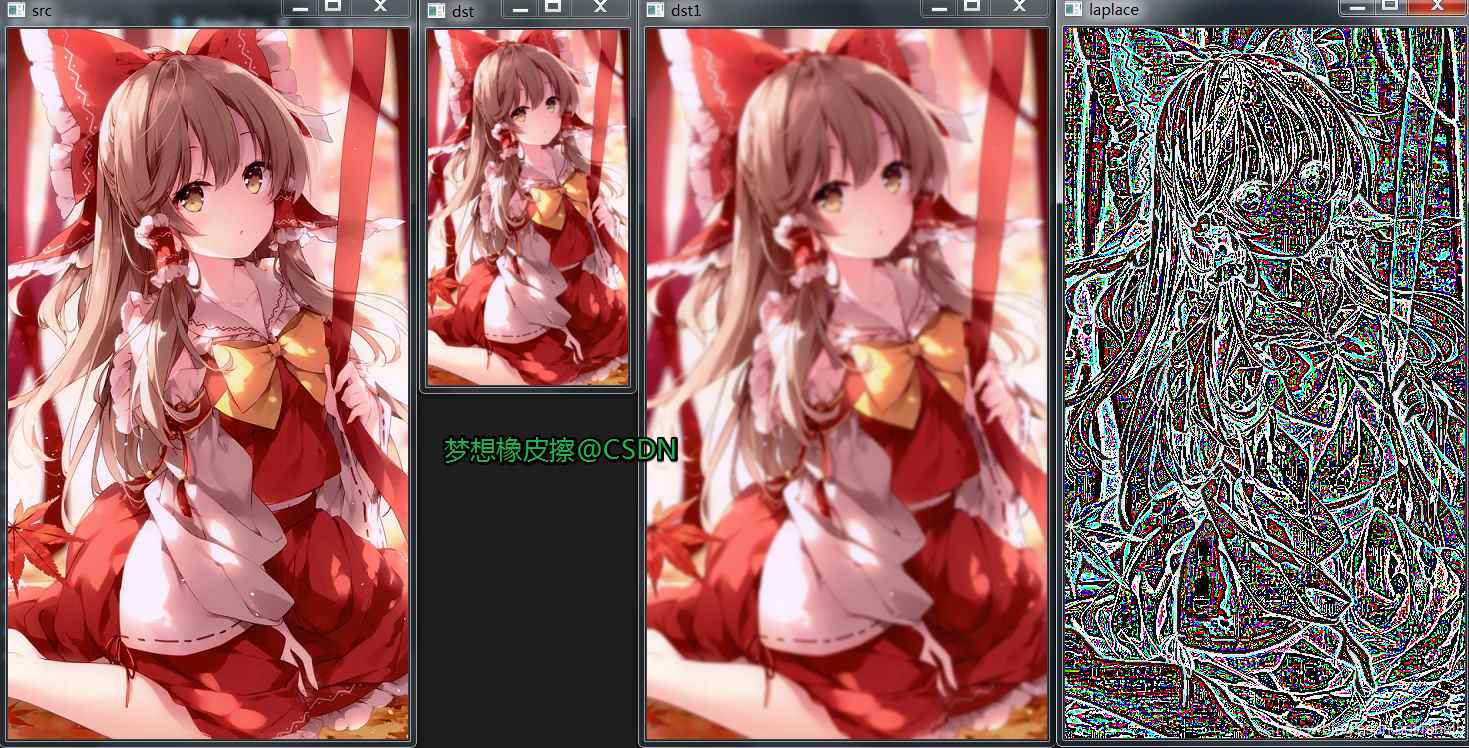
學習過程中發現這樣一段話：圖像尺寸最好是 2 的整次冪，如 256,512 等，否則在金字塔向上的過程中圖像的尺寸會不等，這會導致在拉普拉斯金字塔處理時由于不同尺寸矩陣相減而出錯。

這個我在實測的時候發現確實如此，例如案例中使用的圖像，在向下采樣 2 次的時候，圖像的尺寸就會發生變化，測試代碼如下：

import cv2 as cv

src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采樣1次
dst1 = cv.pyrDown(src)
print(dst1.shape[:2])
cv.imshow("dst", dst1)
# 向下采樣2次
dst2 = cv.pyrDown(dst1)
print(dst1.shape[:2])
cv.imshow("dst2", dst2)

# 向上采樣1次
up_dst1 = cv.pyrUp(dst2)
print(up_dst1.shape[:2])
cv.imshow("up_dst1", up_dst1)

# 計算拉普拉斯金字塔圖像
# 采樣1次 - 向上采樣1次的圖
laplace = dst1 - up_dst1
cv.imshow("laplace", laplace)
cv.waitKey()

注意 print(up_dst1.shape[:2]) 部分的輸出如下：

(710, 400)
(355, 200)
(355, 200)
(356, 200)

如果在該基礎上使用拉普拉斯圖像金字塔，就會出現如下錯誤

Sizes of input arguments do not match

在總結一下拉普拉斯圖像金字塔的執行過程：

• 向下采樣：用高斯金字塔的第 i 層減去 i+1 層做上采樣的圖像，得到拉普拉斯第 i 層的圖像；
• 向上采樣：用高斯金字塔的 i+1 層向上采樣加上拉普拉斯的第 i 層，得到第 i 層的原始圖像。

向下采樣上面的代碼已經實現了，但是拉普拉斯向上采樣還未實現，完善一下代碼如下，為了代碼清晰，我們將變量命名進行修改。

import cv2 as cv

src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 高斯金字塔第 0 層
gus0 = src # 原圖
# 高斯金字塔第 1 層
gus1 = cv.pyrDown(gus0)
# 高斯第 2 層
gus2 = cv.pyrDown(gus1)

# 拉普拉斯金字塔第 0 層
lap0 = gus0 - cv.pyrUp(gus1)
# 拉普拉斯金字塔第 1 層
lap1 = gus1 - cv.pyrUp(gus2)

# 顯示拉普拉斯第一層代碼
cv.imshow("laplace", lap1)
cv.waitKey()

下面用修改好的代碼完成還原圖片的操作。

import cv2 as cv

src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 高斯金字塔第 0 層
gus0 = src # 原圖
# 高斯金字塔第 1 層
gus1 = cv.pyrDown(gus0)
# 高斯第 2 層
gus2 = cv.pyrDown(gus1)


# 拉普拉斯金字塔第 0 層
lap0 = gus0 - cv.pyrUp(gus1)
# 拉普拉斯金字塔第 1 層
lap1 = gus1 - cv.pyrUp(gus2)

rep = lap0 + cv.pyrUp(lap1 + cv.pyrUp(gus2))
gus_rep = cv.pyrUp(cv.pyrUp(gus2))

cv.imshow("rep", rep)
cv.imshow("gus_rep", gus_rep)
cv.waitKey()

以上代碼最重要的部分為下面兩句：

rep = lap0 + cv.pyrUp(lap1 + cv.pyrUp(gus2))
gus_rep = cv.pyrUp(cv.pyrUp(gus2))

第一行代碼中 lap1 + cv.pyrUp(gus2) 即文字公式 【用高斯金字塔的 i+1 層向上采樣加上拉普拉斯的第 i 層，得到第 i 層的原始圖像】的翻譯。

第二行代碼是使用直接向上采樣，最終得到的是損失細節的圖像。

上述代碼運行的結果如下，通過拉普拉斯可以完美還原圖像。

學習本案例之后，你可以在復盤本文開始部分的代碼，將其進行修改。

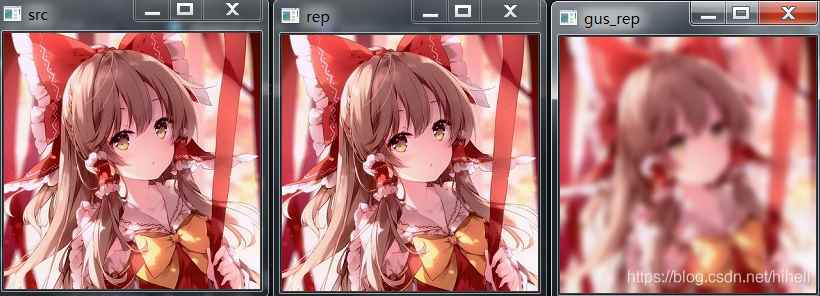
最后在學習一種技巧，可以直接將兩幅圖片呈現，代碼如下：

import cv2 as cv
import numpy as np
src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采樣1次
down_dst1 = cv.pyrDown(src)
print(down_dst1.shape[:2])
cv.imshow("dst", down_dst1)


# 向上采樣1次
up_dst1 = cv.pyrUp(down_dst1)
print(up_dst1.shape[:2])
cv.imshow("up_dst1", up_dst1)

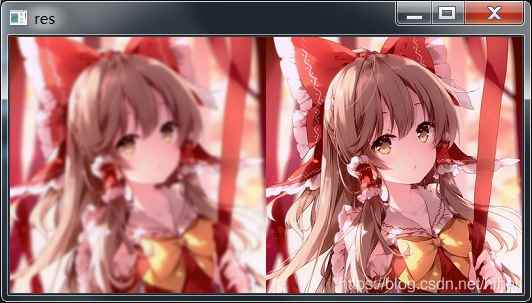
res = np.hstack((up_dst1, src))
cv.imshow('res', res)

cv.waitKey()

運行之后，通過 np.hstack((up_dst1, src))函數，將兩個圖像矩陣合并，實現效果如下：

到此這篇關于Python OpenCV高斯金字塔與拉普拉斯金字塔的實現的文章就介紹到這了,更多相關Python OpenCV金字塔內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家！