數據標準化是機器學習、數據挖掘中常用的一種方法。包括我自己在做深度學習方面的研究時,數據標準化是最基本的一個步驟。
數據標準化主要是應對特征向量中數據很分散的情況,防止小數據被大數據(絕對值)吞并的情況。
另外,數據標準化也有加速訓練,防止梯度爆炸的作用。
下面是從李宏毅教授視頻中截下來的兩張圖。
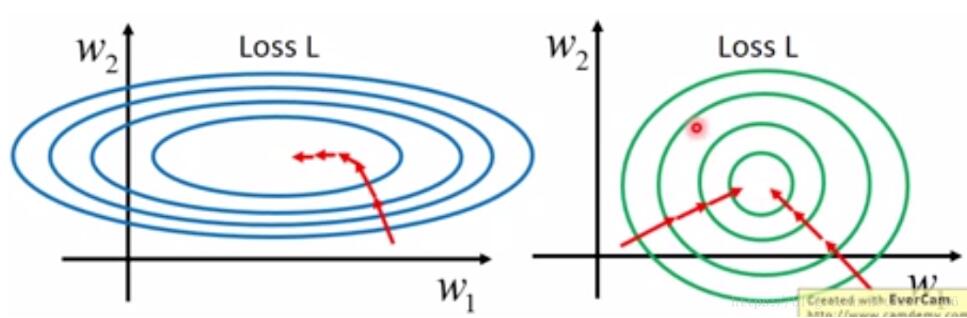
左圖表示未經過數據標準化處理的loss更新函數,右圖表示經過數據標準化后的loss更新圖。可見經過標準化后的數據更容易迭代到最優點,而且收斂更快。
一、[0, 1] 標準化
[0, 1] 標準化是最基本的一種數據標準化方法,指的是將數據壓縮到0~1之間。
標準化公式如下
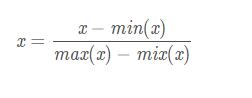
代碼實現
def MaxMinNormalization(x, min, max):
"""[0,1] normaliaztion"""
x = (x - min) / (max - min)
return x
或者
def MaxMinNormalization(x):
"""[0,1] normaliaztion"""
x = (x - np.min(x)) / (np.max(x) - np.min(x))
return x
二、Z-score標準化
Z-score標準化是基于數據均值和方差的標準化化方法。標準化后的數據是均值為0,方差為1的正態分布。這種方法要求原始數據的分布可以近似為高斯分布,否則效果會很差。
標準化公式如下
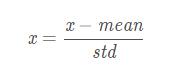
下面,我們看看為什么經過這種標準化方法處理后的數據為是均值為0,方差為1
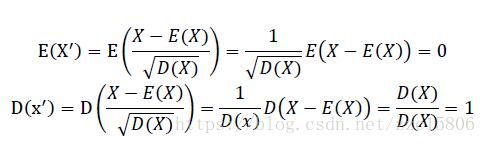
代碼實現
def ZscoreNormalization(x, mean_, std_):
"""Z-score normaliaztion"""
x = (x - mean_) / std_
return x
或者
def ZscoreNormalization(x):
"""Z-score normaliaztion"""
x = (x - np.mean(x)) / np.std(x)
return x
補充:Python數據預處理:徹底理解標準化和歸一化
數據預處理
數據中不同特征的量綱可能不一致,數值間的差別可能很大,不進行處理可能會影響到數據分析的結果,因此,需要對數據按照一定比例進行縮放,使之落在一個特定的區域,便于進行綜合分析。
常用的方法有兩種:
最大 - 最小規范化:對原始數據進行線性變換,將數據映射到[0,1]區間
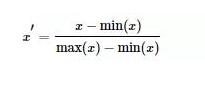
Z-Score標準化:將原始數據映射到均值為0、標準差為1的分布上
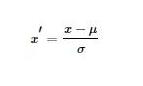
為什么要標準化/歸一化?
提升模型精度:標準化/歸一化后,不同維度之間的特征在數值上有一定比較性,可以大大提高分類器的準確性。
加速模型收斂:標準化/歸一化后,最優解的尋優過程明顯會變得平緩,更容易正確的收斂到最優解。
如下圖所示:
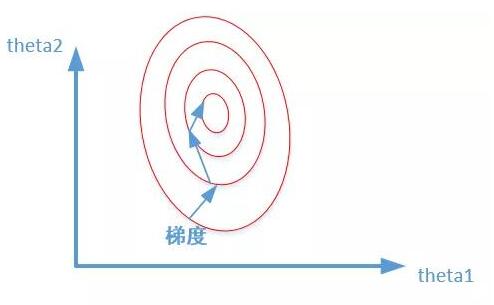
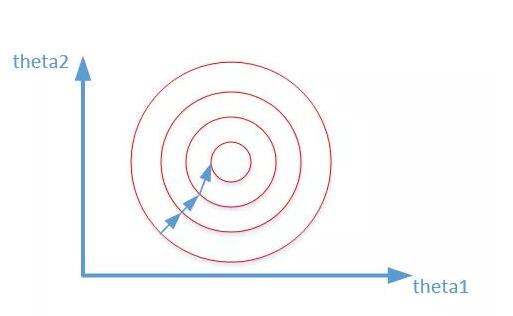
哪些機器學習算法需要標準化和歸一化
1)需要使用梯度下降和計算距離的模型要做歸一化,因為不做歸一化會使收斂的路徑程z字型下降,導致收斂路徑太慢,而且不容易找到最優解,歸一化之后加快了梯度下降求最優解的速度,并有可能提高精度。比如說線性回歸、邏輯回歸、adaboost、xgboost、GBDT、SVM、NeuralNetwork等。需要計算距離的模型需要做歸一化,比如說KNN、KMeans等。
2)概率模型、樹形結構模型不需要歸一化,因為它們不關心變量的值,而是關心變量的分布和變量之間的條件概率,如決策樹、隨機森林。

徹底理解標準化和歸一化
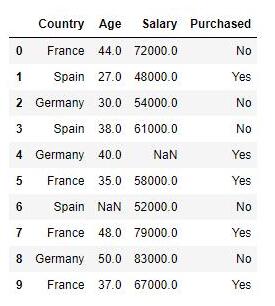
示例數據集包含一個自變量(已購買)和三個因變量(國家,年齡和薪水),可以看出用薪水范圍比年齡寬的多,如果直接將數據用于機器學習模型(比如KNN、KMeans),模型將完全有薪水主導。
#導入數據
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv('Data.csv')
缺失值均值填充,處理字符型變量
df['Salary'].fillna((df['Salary'].mean()), inplace= True)
df['Age'].fillna((df['Age'].mean()), inplace= True)
df['Purchased'] = df['Purchased'].apply(lambda x: 0 if x=='No' else 1)
df=pd.get_dummies(data=df, columns=['Country'])
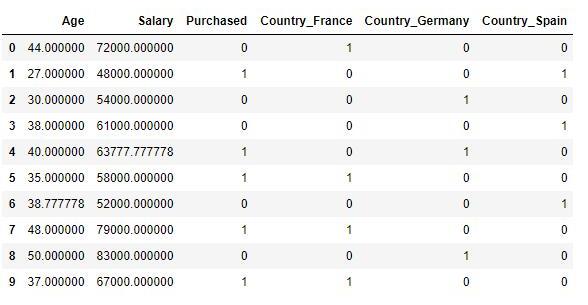
最大 - 最小規范化
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(df)
scaled_features = scaler.transform(df)
df_MinMax = pd.DataFrame(data=scaled_features, columns=["Age", "Salary","Purchased","Country_France","Country_Germany", "Country_spain"])
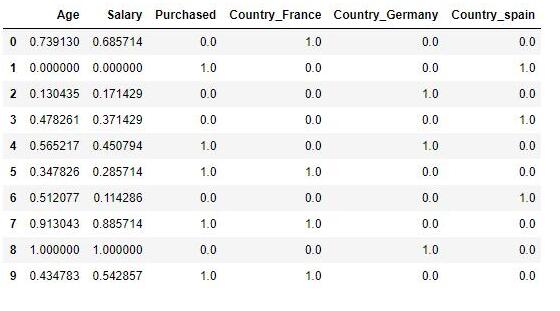
Z-Score標準化
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
sc_X = sc_X.fit_transform(df)
sc_X = pd.DataFrame(data=sc_X, columns=["Age", "Salary","Purchased","Country_France","Country_Germany", "Country_spain"])
import seaborn as sns
import matplotlib.pyplot as plt
import statistics
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
fig,axes=plt.subplots(2,3,figsize=(18,12))
sns.distplot(df['Age'], ax=axes[0, 0])
sns.distplot(df_MinMax['Age'], ax=axes[0, 1])
axes[0, 1].set_title('歸一化方差:% s '% (statistics.stdev(df_MinMax['Age'])))
sns.distplot(sc_X['Age'], ax=axes[0, 2])
axes[0, 2].set_title('標準化方差:% s '% (statistics.stdev(sc_X['Age'])))
sns.distplot(df['Salary'], ax=axes[1, 0])
sns.distplot(df_MinMax['Salary'], ax=axes[1, 1])
axes[1, 1].set_title('MinMax:Salary')
axes[1, 1].set_title('歸一化方差:% s '% (statistics.stdev(df_MinMax['Salary'])))
sns.distplot(sc_X['Salary'], ax=axes[1, 2])
axes[1, 2].set_title('StandardScaler:Salary')
axes[1, 2].set_title('標準化方差:% s '% (statistics.stdev(sc_X['Salary'])))
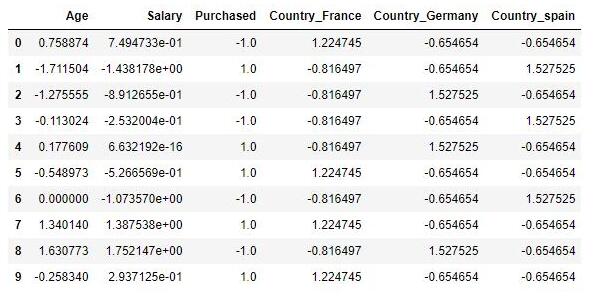
可以看出歸一化比標準化方法產生的標準差小,使用歸一化來縮放數據,則數據將更集中在均值附近。這是由于歸一化的縮放是“拍扁”統一到區間(僅由極值決定),而標準化的縮放是更加“彈性”和“動態”的,和整體樣本的分布有很大的關系。
所以歸一化不能很好地處理離群值,而標準化對異常值的魯棒性強,在許多情況下,它優于歸一化。
以上為個人經驗,希望能給大家一個參考,也希望大家多多支持腳本之家。如有錯誤或未考慮完全的地方,望不吝賜教。
您可能感興趣的文章:- 詳解python實現數據歸一化處理的方式:(0,1)標準化
- python數據預處理之數據標準化的幾種處理方式
- python數據分析數據標準化及離散化詳解